练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】用一条长5米的绳子围成一个长方形，长和宽的比是3：2，面积是（ ）。

    A. 6平方米 B. 5平方米 C. 2.5平方米 D. 1.5平方米

    【答案】D

    【解析】一份是：5÷2÷（3+2）
    =2.5÷5
    =0.5（米）
    长是：0.5×3=1.5（米）
    宽是：0.5×2=1（米）
    面积是：1.5×1=1.5（平方米），
    故选D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】刘师傅要检验一个零件是否为平行四边形，用下列方法不能检验的是( )

    A.AB∥CD，AB=CDB.AB∥CD，AD=BC

    C.AB=CD，AD = BCD.AB∥CD，AD∥BC

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】据报道，2016年汕头市固定资产投资总额、社会消费品零售总额均突破1500亿元，将1500亿用科学记数法可表示为（　　）

    A. 1.5×1011 B. 1.5×1012 C. 15×1011 D. 0.15×1012

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】以长分别为3, 4, 5, 6的四段木棒为边摆三角形，可摆出几种不同的三角形（ ）

    A. 1种B. 2种C. 3种D. 4种

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，已知抛物线（b，c为常数）的顶点为P，等腰直角三角形ABC的顶点A的坐标为（0，﹣1），C的坐标为（4，3），直角顶点B在第四象限．

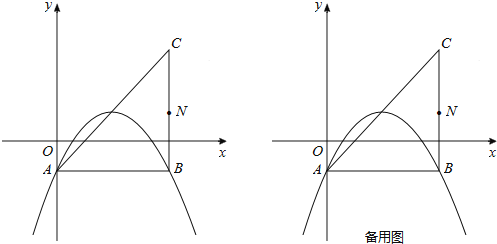
    （1）如图，若该抛物线过A，B两点，求该抛物线的函数表达式；

    （2）平移（1）中的抛物线，使顶点P在直线AC上滑动，且与AC交于另一点Q．

    （i）若点M在直线AC下方，且为平移前（1）中的抛物线上的点，当以M、P、Q三点为顶点的三角形是等腰直角三角形时，求出所有符合条件的点M的坐标；

    （ii）取BC的中点N，连接NP，BQ．试探究是否存在最大值？若存在，求出该最大值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小丽妈妈把5000元钱存到银行，定期三年，年利率是2.25%（税率忽略）。到期时她应得利息是_________元。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，已知正方形ABCD，直角三角形纸板的一个锐角顶点与点A重合，纸板绕点A旋转时，直角三角形纸板的一边与直线CD交于E，分别过B、D作直线AE的垂线，垂足分别为F、G．

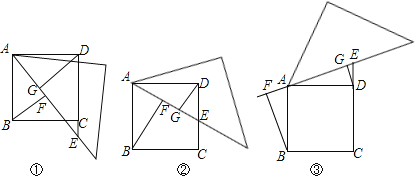
    （1）当点E在DC延长线时，如图①，求证：BF=DG﹣FG；

    （2）将图①中的三角板绕点A逆时针旋转得图②、图③，此时BF、FG、DG之间又有怎样的数量关系？请直接写出结论（不必证明）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校对该校七年级（1）班全体学生的血型做了一次全面调查，根据调查结果绘制了下列两幅不完整的统计图，请你根据统计图提供的信息解答以下问题：

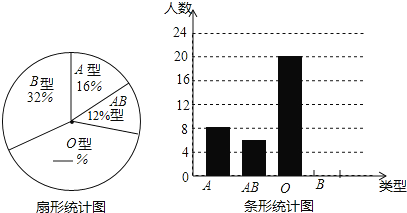
    （1）该校七年级（1）班有多少名学生．

    （2）求出扇形统计图中“O型”血所对扇形的圆心角的度数．

    （3）将条形统计图中“B型”血部分的条形图补充完整．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形OABC中，点O为原点，点A的坐标为（0，8），点C的坐标为（6，0）．抛物线经过点A、C，与AB交于点D．

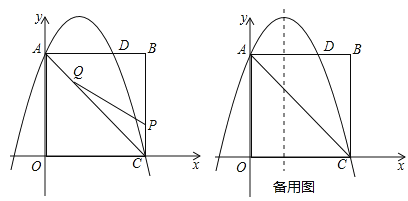
    （1）求抛物线的函数解析式；

    （2）点P为线段BC上一个动点（不与点C重合），点Q为线段AC上一个动点，AQ=CP，连接PQ，设CP=m，△CPQ的面积为S．

    ①求S关于m的函数表达式；

    ②当S最大时，在抛物线的对称轴l上，若存在点F，使△DFQ为直角三角形，请直接写出所有符合条件的点F的坐标；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案