
����Ŀ����ƽ��ֱ������ϵ�У���֪������![]() ��b��cΪ�������Ķ���ΪP������ֱ��������ABC�Ķ���A������Ϊ��0����1����C������Ϊ��4��3����ֱ�Ƕ���B�ڵ������ޣ�
��b��cΪ�������Ķ���ΪP������ֱ��������ABC�Ķ���A������Ϊ��0����1����C������Ϊ��4��3����ֱ�Ƕ���B�ڵ������ޣ�
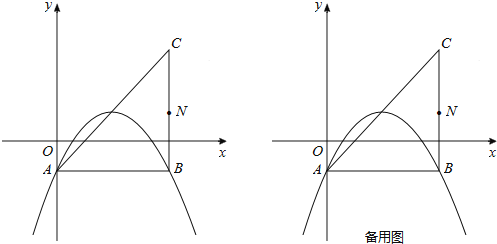
��1����ͼ�����������߹�A��B���㣬��������ߵĺ�������ʽ��
��2��ƽ�ƣ�1���е������ߣ�ʹ����P��ֱ��AC�ϻ���������AC������һ��Q��
��i������M��ֱ��AC�·�����Ϊƽ��ǰ��1���е��������ϵĵ㣬����M��P��Q����Ϊ������������ǵ���ֱ��������ʱ��������з��������ĵ�M�����ꣻ
��ii��ȡBC���е�N������NP��BQ����̽��![]() �Ƿ�������ֵ�������ڣ���������ֵ���������ڣ���˵�����ɣ�
�Ƿ�������ֵ�������ڣ���������ֵ���������ڣ���˵�����ɣ�
���𰸡���1��![]() ����2����i��M1��4����1����M2����2����7����M3��
����2����i��M1��4����1����M2����2����7����M3��![]() ��
��![]() ����M4��
����M4��![]() ��
��![]() ������ii��
������ii��![]() ��
��
��������
�����������1���������B�����꣬Ȼ�����ô���ϵ������������ߵĺ�������ʽ��
��2����i���������ֱ��AC�Ľ���ʽ���߶�PQ�ij��ȣ���Ϊ��������Ļ�����
����MPQΪ����ֱ�������Σ���ɷ�Ϊ�������������
�ٵ�PQΪֱ�DZ�ʱ����M��PQ�ľ���Ϊ![]() ����ʱ����ֱ��AC����ƽ��4����λ������ֱ�ߣ�y=x��5���������ߵĽ��㣬��Ϊ����֮M�㣻
����ʱ����ֱ��AC����ƽ��4����λ������ֱ�ߣ�y=x��5���������ߵĽ��㣬��Ϊ����֮M�㣻
�ڵ�PQΪб��ʱ����M��PQ�ľ���Ϊ![]() ����ʱ����ֱ��AC����ƽ��2����λ������ֱ�ߣ�y=x��3���������ߵĽ��㣬��Ϊ����֮M�㣮
����ʱ����ֱ��AC����ƽ��2����λ������ֱ�ߣ�y=x��3���������ߵĽ��㣬��Ϊ����֮M�㣮
��ii���ɣ�i����֪��PQ=![]() Ϊ��ֵ����˵�NP+BQȡ��Сֵʱ��
Ϊ��ֵ����˵�NP+BQȡ��Сֵʱ��![]() �����ֵ��
�����ֵ��
���ͼ2��ʾ������B����ֱ��AC�ĶԳƵ�B�䣬�ɷ�����֪����B�䡢Q��F��AB�е㣩���㹲��ʱ��NP+BQ��С����СֵΪ�߶�B��F�ij��ȣ�
�����������1��������ֱ��������ABC�Ķ���A������Ϊ��0����1����C������Ϊ��4��3��
����B��������4����1����
�������߹�A��0����1����B��4����1�����㣬�� ����ã�b=2��c=��1���������ߵĺ�������ʽΪ��
����ã�b=2��c=��1���������ߵĺ�������ʽΪ��![]() ��
��
��2����i��
��A��0��1����C��4��3������lAC��y=x��1���������߶���P��ֱ��AC�ϣ���P��t��t��1�����������߱���ʽ��![]() ����lAC�������ߵĽ���Q��t��2��t��3������һM��P��Q����Ϊ������������ǵ���ֱ�������Σ�P��t��t��1����
����lAC�������ߵĽ���Q��t��2��t��3������һM��P��Q����Ϊ������������ǵ���ֱ�������Σ�P��t��t��1����
�ٵ�MΪֱ�Ƕ���ʱ��M��t��t��3����![]() ����t=
����t=![]() ����M1��
����M1��![]() ��
��![]() ����M2��
����M2��![]() ��
��![]() ����
����
�ڵ�QΪֱ�Ƕ���ʱ����M����Ϊ��P�Ƶ�Q˳ʱ����ת90����ɣ�����Q��t��2��t��3��ƽ����ԭ��Q�䣨0��0�������Pƽ�ƺ�P�䣨2��2��������P����ԭ��˳ʱ����ת90�㣬���M�䣨2����2������Q�䣨0��0��ƽ������Q��t��2��t��3�������M��ƽ�ƺ�Ϊ��M��t��t��5������![]() ����t1=4��t2=��2����M1��4����1����M2����2����7����
����t1=4��t2=��2����M1��4����1����M2����2����7����
�۵�PΪֱ�Ƕ���ʱ��ͬ���ɵ�M1��4����1����M2����2����7�����������������з��������ĵ�M������Ϊ��
M1��4����1����M2����2����7����M3��![]() ��
��![]() ����M4��
����M4��![]() ��
��![]() ����
����
��ii��![]() �������ֵ���������£�
�������ֵ���������£�
����i��֪PQ=![]() Ϊ��ֵ����NP+BQȡ��Сֵʱ��
Ϊ��ֵ����NP+BQȡ��Сֵʱ��![]() �����ֵ��
�����ֵ��
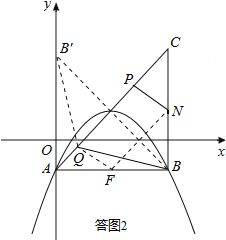
���ͼ2��ȡ��B����AC�ĶԳƵ�B�䣬�õ�B�������Ϊ��0��3����BQ=B��Q��
����QF��FN��QB�䣬��FN��PQ����FN=PQ�����ı���PQFNΪƽ���ı��Σ���NP=FQ����NP+BQ=FQ+B��Q��FB��=![]() =
=![]() ������B�䡢Q��F���㹲��ʱ��NP+BQ��С����СֵΪ
������B�䡢Q��F���㹲��ʱ��NP+BQ��С����СֵΪ![]() ����
����![]() �����ֵΪ
�����ֵΪ![]() =
=![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�������ε�����������ǣ�����������ǣ� ��
A. ��������� B. ֱ�������� C. �۽������� D. ����ȷ����ʲô������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC����DEF�����������Ϊ4��25������ABC����DEF�����Ʊ�Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����һ��ֱ�������ε�����ֱ�DZ�AB��8 cm��BC��6 cm�����Ե�BΪԲ�ģ���ijһֱ�DZ߳�Ϊ�뾶��Բ���� ( )
A. ����A�ڡ�B�ϣ����C�ڡ�B�� B. ����C�ڡ�B�ϣ����A�ڡ�B��
C. ����A�ڡ�B�ϣ����C�ڡ�B�� D. ���϶�����ȷ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����5������Χ��һ�������Σ����Ϳ��ı���3��2������ǣ� ����
A. 6ƽ���� B. 5ƽ���� C. 2.5ƽ���� D. 1.5ƽ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������ֱ�������Σ��������ȷ������( )
����֪һֱ�DZ���Խǡ�����֪����ǡ�����֪б�ߺ�һ��ǡ�����֪һֱ�DZߺ�һб��
A. �٢ڢ� B. �ڢ� C. �ڢ� D. ֻ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���糿��̩ɽ����Ϊ����5�棬��������7�棬�����½�8�棬��̩ɽ�������¶��� �� ��
A. ����4 �� B. ����4�� C. ���� 6�� D. ����6��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]() ��ͼ����ͼ��ʾ��������5�����ۣ���abc��0����b��a+c����4a+2b+c��0����2a+b=0����a+b��m��am+b����m��1��ʵ������������ȷ�Ľ����У� ��
��ͼ����ͼ��ʾ��������5�����ۣ���abc��0����b��a+c����4a+2b+c��0����2a+b=0����a+b��m��am+b����m��1��ʵ������������ȷ�Ľ����У� ��
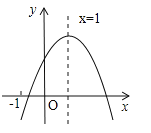
A��2�� B��3�� C��4�� D��5��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com