Question

【题目】如图所示，已知正方形ABCD，直角三角形纸板的一个锐角顶点与点A重合，纸板绕点A旋转时，直角三角形纸板的一边与直线CD交于E，分别过B、D作直线AE的垂线，垂足分别为F、G．

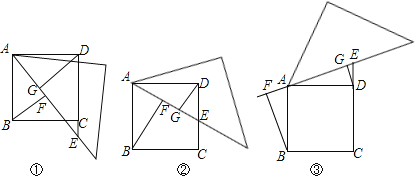
（1）当点E在DC延长线时，如图①，求证：BF=DG﹣FG；

（2）将图①中的三角板绕点A逆时针旋转得图②、图③，此时BF、FG、DG之间又有怎样的数量关系？请直接写出结论（不必证明）

Answer 1

【答案】（1）证明见解析；（2）图2：BF=DG+FG，图3：BF=FG﹣DG．

【解析】

试题分析：（1）如图①，由四边形ABCD是正方形，可得AB=AD，由B、D作直线AE的垂线，垂足分别为F、G．可得∠AFB=∠DGA=90°由角的关系可得∠ABF=∠GAD，可得△ABF≌△ADG可得BF=AG，AF=DG，利用AG=AF﹣FG；即可证得BF=DG﹣FG；

（2）如图②，由四边形ABCD是正方形，可得AB=AD，由B、D作直线AE的垂线，垂足分别为F、G．可得∠AFB=∠DGA=90°由角的关系可得∠ABF=∠GAD，可得△ABF≌△ADG可得BF=AG，AF=DG，利用AG=AF+FG，可得BF=DG+FG；如图③，由四边形ABCD是正方形，可得AB=AD，由B、D作直线AE的垂线，垂足分别为F、G．可得∠AFB=∠DGA=90°由角的关系可得∠ABF=∠GAD，可得△ABF≌△ADG可得BF=AG，AF=DG，利用AG=FG﹣AF，可得BF=FG﹣DG．

试题解析：（1）如图①，∵四边形ABCD是正方形，∴AB=AD，∵B、D作直线AE的垂线，垂足分别为F、G，∴∠AFB=∠DGA=90°，∵∠BAF+∠GAD=90°，∠BAF+∠ABF=90°，∴∠ABF=∠GAD，在△ABF和△ADG中，∵∠AFB=∠DGA，∠ABF=∠DAG，AB=AD，∴△ABF≌△ADG（AAS），∴BF=AG，AF=DG，∵AG=AF﹣FG，∴BF=DG﹣FG；

（2）如图②，∵四边形ABCD是正方形，∴AB=AD，∵B、D作直线AE的垂线，垂足分别为F、G，∴∠AFB=∠DGA=90°，∵∠BAF+∠GAD=90°，∠BAF+∠ABF=90°，∴∠ABF=∠DAG，在△ABF和△ADG中，∵∠AFB=∠DGA，∠ABF=∠DAG，AB=AD，∴△ABF≌△ADG（AAS），∴BF=AG，AF=DG，∵AG=AF+FG，∴BF=DG+FG；

如图③，∵四边形ABCD是正方形，∴AB=AD，∵B、D作直线AE的垂线，垂足分别为F、G，∴∠AFB=∠DGA=90°，∵∠BAF+∠GAD=90°，∠BAF+∠ABF=90°，∴∠ABF=∠DAG，在△ABF和△ADG中，∵∠AFB=∠DGA，∠ABF=∠DAG，AB=AD，∴△ABF≌△ADG（AAS），∴BF=AG，AF=DG，∵AG=FG﹣AF，∴BF=FG﹣DG．