
分析 根据$\frac{2}{{x}^{2}-1}$+$\frac{20}{{x}^{2}-100}$=$\frac{1}{x-1}$-$\frac{1}{x+1}$+$\frac{1}{x-10}$-$\frac{1}{x+10}$、$\frac{11}{(x-1)(x+10)}$+$\frac{11}{(x-10)(x+1)}$=$\frac{1}{x-1}-\frac{1}{x+10}$+$\frac{1}{x-10}$-$\frac{1}{x+1}$得$\frac{2}{{x}^{2}-1}$+$\frac{20}{{x}^{2}-100}$=$\frac{11}{(x-1)(x+10)}$+$\frac{11}{(x-10)(x+1)}$,同理知等式左右两边的具有此规律的每两项均相等,即可得证.
解答 证明:∵$\frac{2}{{x}^{2}-1}$+$\frac{20}{{x}^{2}-100}$=$\frac{2}{(x+1)(x-1)}$+$\frac{20}{(x+10)(x-10)}$=$\frac{1}{x-1}$-$\frac{1}{x+1}$+$\frac{1}{x-10}$-$\frac{1}{x+10}$,
$\frac{11}{(x-1)(x+10)}$+$\frac{11}{(x-10)(x+1)}$=$\frac{1}{x-1}-\frac{1}{x+10}$+$\frac{1}{x-10}$-$\frac{1}{x+1}$,
∴$\frac{2}{{x}^{2}-1}$+$\frac{20}{{x}^{2}-100}$=$\frac{11}{(x-1)(x+10)}$+$\frac{11}{(x-10)(x+1)}$,
同理,$\frac{4}{{x}^{2}-4}$+$\frac{18}{{x}^{2}-81}$=$\frac{11}{(x-2)(x+9)}$+$\frac{11}{(x-9)(x+2)}$,
…
∴$\frac{2}{{x}^{2}-1}$+$\frac{4}{{x}^{2}-4}$+$\frac{6}{{x}^{2}-9}$+…+$\frac{20}{{x}^{2}-100}$=$\frac{11}{(x-1)(x+10)}$+$\frac{11}{(x-2)(x+9)}$+…+$\frac{11}{(x-10)(x+1)}$.
点评 本题主要考查分式的化简求值,熟练掌握异分母分式运算的法则是关键.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:选择题
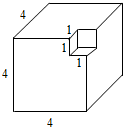 如图,有一个棱长是4cm的正方体,从它的一个顶点处挖去一个棱长是1cm的正方体后,剩下物体的表面积和原来的表面积相比较( )
如图,有一个棱长是4cm的正方体,从它的一个顶点处挖去一个棱长是1cm的正方体后,剩下物体的表面积和原来的表面积相比较( )| A. | 变大了 | B. | 变小了 | C. | 没变 | D. | 无法确定变化 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 抛物线y=-$\frac{1}{4}$x2+$\frac{1}{2}$x+2与x轴交于A、B两点,与y轴交于点C.
抛物线y=-$\frac{1}{4}$x2+$\frac{1}{2}$x+2与x轴交于A、B两点,与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com