
 如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA,OB,OC,AC,OB与AC相交于点E,若∠COB=3∠AOB,OC=2$\sqrt{3}$,则图中阴影部分面积为( )
如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA,OB,OC,AC,OB与AC相交于点E,若∠COB=3∠AOB,OC=2$\sqrt{3}$,则图中阴影部分面积为( )| A. | 2$\sqrt{3}$ | B. | 3π-2$\sqrt{3}$ | C. | 3π-4$\sqrt{3}$ | D. | 3π |
分析 根据四边形ABCD是⊙O的内接四边形得到∠ABC+∠D=180°,根据∠ABC=2∠D得到∠D+2∠D=180°,从而求得∠D=60°,最后根据OA=OC得到∠OAC=∠OCA=30°,根据∠COB=3∠AOB得到∠AOB=30°,从而得到∠COB为直角,然后利用S阴影=S扇形OBC-S△OEC求解.
解答 解:∵四边形ABCD是⊙O的内接四边形,
∴∠ABC+∠D=180°,
∵∠ABC=2∠D,
∴∠D+2∠D=180°,
∴∠D=60°,
∴∠AOC=2∠D=120°,
∵OA=OC,
∴∠OAC=∠OCA=30°;
∵∠COB=3∠AOB,
∴∠AOC=∠AOB+3∠AOB=120°,
∴∠AOB=30°,
∴∠COB=∠AOC-∠AOB=90°,
在Rt△OCE中,OC=2$\sqrt{3}$,
∴OE=OC•tan∠OCE=2$\sqrt{3}$•tan30°=2$\sqrt{3}$×$\frac{\sqrt{3}}{3}$=2,
∴S△OEC=$\frac{1}{2}$OE•OC=$\frac{1}{2}$×2×2$\sqrt{3}$=2$\sqrt{3}$,
∴S扇形OBC=$\frac{90•×(2\sqrt{3})^{2}}{360}$=3π,
∴S阴影=S扇形OBC-S△OEC=3π-2$\sqrt{3}$.
故选B.
点评 本题考查了扇形面积的计算,圆内接四边形的性质,解直角三角形的知识,在求不规则的阴影部分的面积时常常转化为几个规则几何图形的面积的和或差.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:选择题
| A. | k>0,b>0 | B. | k>0,b<0 | C. | k<0,b>0 | D. | k<0,b<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,直线l上所有点的坐标都是方程x+y=2的解,直线m上所有点的坐标都是方程x-y=0的解.观察该图回答:直线l与m的交点M的坐标为(1,1).方程组$\left\{\begin{array}{l}{x+y=2}\\{x-y=0}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$.
如图,直线l上所有点的坐标都是方程x+y=2的解,直线m上所有点的坐标都是方程x-y=0的解.观察该图回答:直线l与m的交点M的坐标为(1,1).方程组$\left\{\begin{array}{l}{x+y=2}\\{x-y=0}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
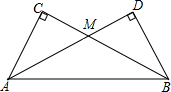 把两个同样大小的含30°角的三角尺像如图所示那样放置,其中M是AD与BC的交点.
把两个同样大小的含30°角的三角尺像如图所示那样放置,其中M是AD与BC的交点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,BE是△ABC的外接圆O的直径,CD是△ABC的高.
已知:如图,BE是△ABC的外接圆O的直径,CD是△ABC的高.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在?ABCD中,点E在DC上,BE与AC相交于点F,若$\frac{DE}{EC}$=$\frac{1}{2}$,则$\frac{BF}{BE}$的值为( )
如图,在?ABCD中,点E在DC上,BE与AC相交于点F,若$\frac{DE}{EC}$=$\frac{1}{2}$,则$\frac{BF}{BE}$的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
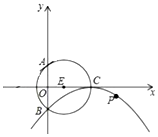 如图,⊙E的圆心E(3,0),半径为5,⊙E与y轴相交于A、B两点(点A在点B的上方),与x轴的正半轴交于点C,直线l的解析式为y=kx+4k+1(k为实数),以点C为顶点的抛物线过点B.
如图,⊙E的圆心E(3,0),半径为5,⊙E与y轴相交于A、B两点(点A在点B的上方),与x轴的正半轴交于点C,直线l的解析式为y=kx+4k+1(k为实数),以点C为顶点的抛物线过点B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com