
��ͼ����ƽ��ֱ������ϵ�У���֪OA=12���ף�OB=6���ף���P�ӵ�O��ʼ��OA�����A��1����/����ٶ��ƶ�����Q�ӵ�B��ʼ��BO�����O��1����/����ٶ��ƶ������P��Qͬʱ��������t���룩��ʾ�ƶ���ʱ�䣨0��t��6������ô
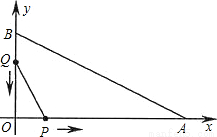
��1�����POQ�����Ϊy����y����t�ĺ�������ʽ��
��2������POQ��������ʱ������POQ��ֱ��PQ���ۺ�õ���PCQ�����жϵ�C�Ƿ�����ֱ��AB�ϣ���˵�����ɣ�
��3����tΪ��ֵʱ����POQ���AOB���ƣ�
��1��y=-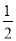 t2+3t��0��t��6������2�� ��C������ֱ��AB�ϣ���3�� ��t=4��t=2ʱ����POQ���AOB���ƣ�
t2+3t��0��t��6������2�� ��C������ֱ��AB�ϣ���3�� ��t=4��t=2ʱ����POQ���AOB���ƣ�
��������
�����������1������P��Q���ٶȣ���ʱ��t��ʾ��OQ��OP�ij�������ͨ�������ε������ʽ�ó�y��t�ĺ�����ϵʽ��
��2���ȸ��ݣ�1���ĺ���ʽ���y���ʱ��x��ֵ�����ɵó�OQ��OP�ij���Ȼ�����C��������ֱ��AB�Ľ���ʽ����C���������ֱ��AB�Ľ���ʽ�м����жϳ�C�Ƿ���AB�ϣ�
��3������Ҫ�֡�OPQ�ס�OAB�͡�OPQ�ס�OBA�������������⣬�ɸ��ݸ��Եó��Ķ�Ӧ�ɱ���������t��ֵ��
�����������1����OA=12��OB=6�������⣬��BQ=1��t=t��OP=1��t=t��
��OQ=6-t��
��y=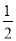 ��OP��OQ=
��OP��OQ=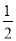 ��t��6-t��=-
��t��6-t��=-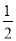 t2+3t��0��t��6����
t2+3t��0��t��6����
��2����y=-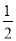 t2+3t��
t2+3t��
�൱y�����ֵʱ��t=3
��OQ=3��OP=3������POQ�ǵ���ֱ�������Σ�
�ѡ�POQ��ֱ��PQ���ۺɵ��ı���OPCQ�������Σ�
���C��������3��3����
��A��12��0����B��0��6����
��ֱ��AB�Ľ���ʽΪy=-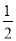 x+6
x+6
��x=3ʱ��y=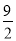 ��3��
��3��
���C������ֱ��AB�ϣ�
��3��������POQ�ס�AOBʱ��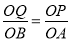 ����
����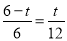 ��
��
12-2t=t��
��t=4��
������POQ�ס�BOAʱ��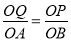 ����
����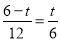
6-t=2t��
��t=2��
��0��t��6��
��t=4��t=2���������⣬
�൱t=4��t=2ʱ����POQ���AOB���ƣ�
���㣺���κ����ۺ��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2014-2015ѧ��ɽ��ʡ��̩�о��꼶��ѧ��ѧҵˮƽģ����ѧ�Ծ��������棩 ���ͣ�ѡ����
����ͼ�ηֱ��ǹ��֡����ϡ����ࡢ��ɽ����̨��̨�գ�����Ϊ���ĶԳ�ͼ�ε��ǣ� ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
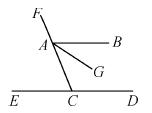
��ͼ��AB��ED,AGƽ�֡�BAC,��ECF=70��, ���FAG�Ķ�����( )
A.155�� B.145�� C.110�� D.35��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ��ɽ��ʡ���꼶��ѧ����ĩ������ѧ�Ծ��������棩 ���ͣ�ѡ����
�ڷ���������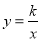 �У���x��0ʱ��y��x���������������κ���
�У���x��0ʱ��y��x���������������κ���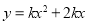 ͼ������ǣ� ��
ͼ������ǣ� ��
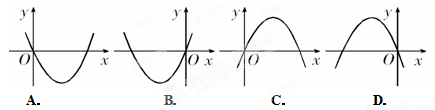
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ��ɽ��ʡ���꼶��ѧ����ĩ������ѧ�Ծ��������棩 ���ͣ�ѡ����
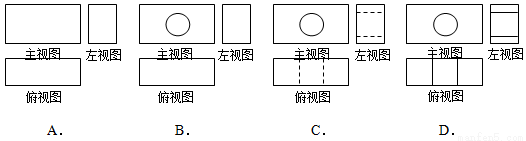
��ͼ��ʾ�ļ������������ͼ�ǣ� ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ����о��꼶12�½β�����ѧ�Ծ��������棩 ���ͣ������
��ͼ���ڱ߳�Ϊ1����������ɵ������У���AOB�Ķ�����ڸ���ϣ����е�A��5��4����B��1��3��������AOB�Ƶ�O��ʱ����ת90���õ���A1OB1��

��1��������A1OB1��
��2������ת�����е�B��������·����Ϊ
��3��������ת�������߶�AB��BOɨ����ͼ�ε����֮�ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ����о��꼶12�½β�����ѧ�Ծ��������棩 ���ͣ������
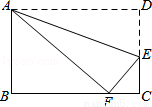
��ͼ��������ABCD��AE�۵�����Dǡ������BC���ϵĵ�F�������AB��AD=2��3����ôtan��EFCֵ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ����о��꼶12�½β�����ѧ�Ծ��������棩 ���ͣ�ѡ����
����������y=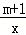 ��ÿ�������ڵĺ���ֵy��x�������������m��ȡֵ��Χ�ǣ� ��
��ÿ�������ڵĺ���ֵy��x�������������m��ȡֵ��Χ�ǣ� ��
A��m��0 B��m��0 C��m����1 D��m����1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�긣��ʡ��͡�س�����У���꼶12��������ѧ�Ծ��������棩 ���ͣ������
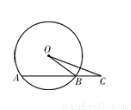
��10�֣���ͼ����O�İ뾶OB��5 cm��AB�ǡ�O���ң���C��AB�ӳ�����һ�㣬�ҡ�OCA��30�㣬OC��8 cm����AB�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com