练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】把长为20，宽为a的长方形纸片(10＜a＜20)，如图那样折一下，剪下一个边长等于长方形宽度的正方形(称为第一次操作)；再把剩下的长方形如图那样折一下，剪下一个边长等于此时长方形宽度的正方形(称为第二次操作)；如此反复操作下去，若在第n次操作后，剩下的长方形为正方形，则操作停止．当n=3时，a的值为________.

    【答案】12或15

    【解析】

    根据操作步骤，可知每一次操作时所得正方形的边长都等于原矩形的宽．所以首先需要判断矩形相邻的两边中，哪一条边是矩形的宽．当10＜a＜20时，矩形的长为20，宽为a，所以第一次操作时所得正方形的边长为a，剩下的矩形相邻的两边分别为20-a，a．由20-a＜a可知，第二次操作时所得正方形的边长为20-a，剩下的矩形相邻的两边分别为20-a，a-（20-a）=2a-20．由于（20-a）-（2a-20）=40-3a，所以（20-a）与（2a-20）的大小关系不能确定，需要分情况进行讨论．又因为可以进行三次操作，故分两种情况：①20-a＞2a-20；②20-a＜2a-20．对于每一种情况，分别求出操作后剩下的矩形的两边，根据剩下的矩形为正方形，列出方程，求出a的值．

    由题意，可知当10＜a＜20时，第一次操作后剩下的矩形的长为a，宽为20-a，所以第二次操作时正方形的边长为20-a，

    第二次操作以后剩下的矩形的两边分别为20-a，2a-20．此时，分两种情况：

    ①如果20-a＞2a-20，即a＜，那么第三次操作时正方形的边长为2a-20．

    ∵经过第三次操作后所得的矩形是正方形，

    ∴矩形的宽等于20-a，

    即2a-20=（20-a）-（2a-20），

    解得a=12；

    ②如果20-a＜2a-20，即a＞，那么第三次操作时正方形的边长为20-a．

    则20-a=（2a-20）-（20-a），

    解得a=15．

    故答案为：12或15.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某工厂餐厅计划购买12张餐桌和一批餐椅，现在从甲、乙两商场了解到，同一型号的餐桌报价每张均为200元，餐椅报价每把均为50元，甲商场做活动，每购买一张餐桌赠送一把餐椅。乙商场的活动是所有桌椅均按报价的八五折销售。若该工厂计划购买餐椅 (＞12)把，则：

    （1）当购买40把餐椅时，到哪家商场购买划算？

    （2）用含的代数式表示到甲、乙两商场购买所需要的费用。

    （3）当购买多少把餐椅时，到甲、乙两商场购买所需要的费用相同？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知点M（n，﹣n ）在第二象限，过点M的直线y=kx+b（0＜k＜1）分别交x轴、y轴于点A，B，过点M作MN⊥x轴于点N，则下列点在线段AN的是（　　）

    A. （（k﹣1）n，0） B. （（k+）n，0）） C. （，0） D. （（k+1）n，0）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，点O是AC边上的一个动点，过点O作直线MN∥BC，设MN交∠BCA的角平分线于点E，交∠BCA的外角平分线于点F．

    （1）求证：EO=FO；

    （2）当点O运动到何处时，四边形AECF是矩形？并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算：

    （1）（-12）-5+（-14）-（-39） （2）

    （3）5(a2b－ab2)－(ab2＋3a2b) （4）（用简便方法计算）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线l经过⊙O的圆心O，且与⊙O交于A、B两点，点C在⊙O上，且∠AOC＝30°，点P是直线l上的一个动点(与圆心O不重合)，直线CP与⊙O相交于另一点Q，如果QP＝QO，则∠OCP＝ ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AC=9，AB=12，BC=15，P为BC边上一动点，PG⊥AC于点G，PH⊥AB于点H．

    (1)求证：四边形AGPH是矩形；

    (2)在点P的运动过程中，GH的长度是否存在最小值？若存在，请求出最小值，若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在锐角内部，画1条射线，可得3个锐角；画2条不同射线，可得6个锐角；画3条不同射线，可得10个锐角；…….照此规律，画6条不同射线，可得锐角________个．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

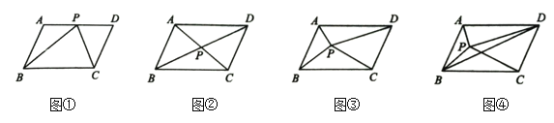
    【题目】如图，四边形是面积为的平行四边形，其中.

    （1）如图①，点为边上任意一点，则的面积和的面积之和与的面积之间的数量关系是__________；

    （2）如图②，设交于点，则的面积和的面积之和与的面积之间的数量关系是___________；

    （3）如图③，点为内任意一点时，试猜想的面积和的面积之和与的面积之间的数量关系，并加以证明；

    （4）如图④，已知点为内任意一点，的面积为，的面积为，连接，求的面积.

    查看答案和解析>>

    同步练习册答案