
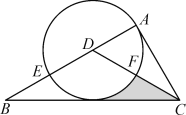
【题目】如图,在Rt△ABC中,∠BAC=90°,CD平分∠ACB,交AB于点D,以点D为圆心,DA为半径的圆与AB相交于点E,与CD交于点F.
(1)求证:BC是⊙D的切线;
(2)若EF∥BC,且BC=6,求图中阴影部分的面积.
【答案】(1)见解析;(2)![]() -
-![]()
【解析】
(1)过D作DG⊥BC于G,根据角平分线的性质得到DG=DA,根据切线的判定定理即可得到结论;
(2)连接EF,由已知和(1)的结论可得DG⊥EF,根据垂径定理、圆心角、弧之间的关系及等量代换可得∠CDG=∠ADC=∠BDG=60°,再求出DG、CG的长,根据阴影部分的面积=△DGC的面积-扇形DGF的面积即可求解.
(1)过D作DG⊥BC于G,
∵DA⊥AC,∠ACD=∠BCD,
∴DG=DA,
∴BC是⊙D的切线.
(2)连接EF,
∵EF∥BC,由(1)DG⊥BC,
∴DG⊥EF,
∴![]() ,
,
∴∠EDG=∠CDG.
由(1)∠ACD=∠BCD,∠ACD+∠ADC=∠BCD+∠CDG=90°,
∴∠CDG=∠ADC,
∴∠CDG=∠ADC=∠BDG=60°.
∵EF∥BC,
∴∠DEF=∠B, ∠DFE=∠DCB,
在⊙D中,DE=DF,
∴∠DFE=∠DEF.
∴∠B=∠DCB,
∴DB=DC.
∵DG⊥BC,
∴CG=![]() BC=3.
BC=3.
在Rt△DCG中,DG=![]() =
=![]() .
.
∴S阴影=![]() ×3×
×3×![]() -
-![]() π(
π(![]() )2=
)2=![]() -
-![]() .
.


科目:初中数学 来源: 题型:
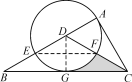
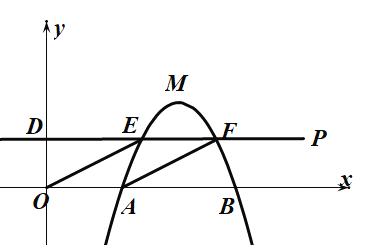
【题目】已知二次函数y=﹣x2+bx+c的图象经过点A(2,0),B(5,0),过点D(0,![]() )作y轴的垂线DP交图象于E、F.
)作y轴的垂线DP交图象于E、F.
(1)求b、c的值和抛物线的顶点M的坐标;
(2)求证:四边形OAFE是平行四边形;
(3)将抛物线向左平移的过程中,抛物线的顶点记为M′,直线DP与抛物线的左交点为E′,连接OM′,OE′,当OE′+OM′的值最小时求直线OE′的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x=![]() ,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2.上述说法正确的是( )
,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2.上述说法正确的是( )

A.①②④ B.③④ C.①③④ D.①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某中学去年中招体育考试中女生”一分钟跳绳”项目的成绩情况,从中抽取部分女生的成绩,绘制出如图所示的频数分布直方图(从左到右依次为第一组到第六组,每小组含最小值,不含最大值)和扇形统计图,请根据下列统计图中提供的信息解决下列问题

(1)本次抽取的女生总人数为 第六小组人数占总人数的百分比为 请补全频数分布直方图;
(2)题中样本数据的中位数落在第 组内;
(3)若“一分钟跳绳”不低于130次的成绩为优秀,这个学校九年级共有女生560人,请估计该校九年级女生“一分钟跳绳”成绩的优秀人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的半径为5,弦AB,CD所对的圆心角分别是∠AOB,∠COD,下列说法正确的是( )①若∠AOB=∠COD,则CD=AB;②若CD=AB,则CD,AB所对的弧相等;③若CD=AB,则点O到CD,AB的距离相等;④若∠AOB+∠COD=180°,且CD=6,则AB=8.

A.①②③④B.①③④C.①②④D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
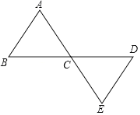
【题目】如图,连接在一起的两个等边三角形的边长都为2cm,一个微型机器人由点A开始按A→B→C→D→E→C→A→B→C…的顺序沿等边三角形的边循环移动.当微型机器人移动了2018cm后,它停在了点_____上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知C(3,4),以点C为圆心的圆与y轴相切.点A、B在x轴上,且OA=OB.点P为⊙C上的动点,∠APB=90°,则AB长度的最大值为_____.
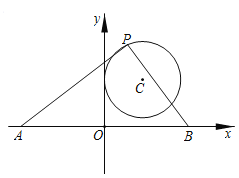
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=5,BC=8,点D是边BC上(不与B,C重合)一动点,∠ADE=∠B=a,DE交AC于点E,下列结论:①AD2=AE.AB;②1.8≤AE<5;⑤当AD=![]() 时,△ABD≌△DCE;④△DCE为直角三角形,BD为4或6.25.其中正确的结论是_____.(把你认为正确结论序号都填上)
时,△ABD≌△DCE;④△DCE为直角三角形,BD为4或6.25.其中正确的结论是_____.(把你认为正确结论序号都填上)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠DAB=45°,AB=2,P为线段AB上一动点,且不与点A重合,过点P作PE⊥AB交AD于点E,将∠A沿PE折叠,点A落在直线AB上点F处,连接DF、CF,当△CDF为等腰三角形时,AP的长是_____.
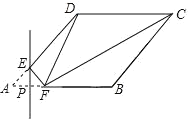
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com