
如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的直线互相垂直,垂足为D,且AC平分∠DAB.
(1)求证:DC为⊙O的切线;
(2)若⊙O的半径为3,AD=4 ,求AC的长.

(1)证明见解析;(2)2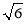 .
.
【解析】
试题分析:(1)连接OC,由OA=OC可以得到∠OAC=∠OCA,然后利用角平分线的性质可以证明∠DAC=∠OCA,接着利用平行线的判定即可得到OC∥AD,然后就得到OC⊥CD,由此即可证明直线CD与⊙O相切于C点;
(2)连接BC,根据圆周角定理的推理得到∠ACB=90°,又∠DAC=∠OAC,由此可以得到△ADC∽△ACB,然后利用相似三角形的性质即可解决问题.
(1)证明:连接OC
∵OA=OC
∴∠OAC=∠OCA
∵AC平分∠DAB
∴∠DAC=∠OAC
∴∠DAC=∠OCA
∴OC∥AD
∵AD⊥CD
∴OC⊥CD
∴直线CD与⊙O相切于点C;
(2)连接BC,则∠ACB=90°.
∵∠DAC=∠OAC,∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴ ,
,
∴AC2=AD•AB,
∵⊙O的半径为3,AD=4,
∴AB=6,
∴AC=2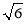 .
.
考点:1.切线的判定;2.相似三角形的判定与性质.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2013-2014学年安徽省当涂县四校九年级上学期期末联考数学试卷(解析版) 题型:解答题
如图,已知△ABC中,∠ACB=90°,AC=BC,点E、F在AB上,∠ECF=45°.求证:△ACF∽△BEC;

查看答案和解析>>
科目:初中数学 来源:2013-2014学年四川省眉山市华兴联谊学校九年级下学期期中考试数学试卷(解析版) 题型:解答题
已知直角坐标系中有一点A(-4,3),点B在x轴上,△AOB是等腰三角形。
(1)求满足条件的所有点B的坐标。(直接写出答案)
(2)求过O、A、B三点且开口向下的抛物线的函数解析式。(只需求出满足条件的即可)。
(3)在(2)中求出的抛物线上存在点p,使得以O、A、B、P四点为顶点的四边形是梯形,求满足条件的所有点P的坐标及相应梯形的面积。

查看答案和解析>>
科目:初中数学 来源:2013-2014学年四川省眉山市华兴联谊学校九年级下学期期中考试数学试卷(解析版) 题型:选择题
下列事件中是必然事件的是( )
A、一个直角三角形的两个锐角分别是40°和60°
B、抛掷一枚硬币,落地后正面朝上。
C、当x是非负数时,x≥0
D、长为5cm、5cm、11cm的三条线段能围成一个三角形。
查看答案和解析>>
科目:初中数学 来源:2013-2014学年四川省眉山市华兴联谊学校九年级下学期期中考试数学试卷(解析版) 题型:选择题
2010年某景区全年游客人数超8030000人次,8030000用科学计数法表示是( )
A、803×104 B、80.3×105 C、8.03×106 D、8.03×107
查看答案和解析>>
科目:初中数学 来源:2013-2014学年四川省乐山市夹江县九年级毕业会考适应性考试数学试卷(解析版) 题型:解答题
有一人患了流感,经过两轮传染后共有64人患了流感.
(1)求每轮传染中平均一个人传染了几个人?
(2)如果不及时控制,第三轮将又有多少人被传染?
查看答案和解析>>
科目:初中数学 来源:2013-2014学年吉林省长春市朝阳区中考一模数学试卷(解析版) 题型:解答题
周末,小强在文化广场放风筝.如图,小强为了计算风筝离地面的高度,他测得风筝的仰角为58°,已知风筝线BC的长为10米,小强的身高AB为1.55米.请你帮小强画出测量示意图,并计算出风筝离地面的高度(结果精确到0.1米).(参考数据:sin58°=0.85,cos58°=0.53,tan58°=1.60)
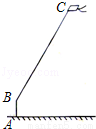 ]
]
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市顺义区中考二模数学试卷(解析版) 题型:选择题
某中学九(1)班6个同学在课间体育活动时进行1分钟跳绳比赛,跳绳个数如下:
126,144,134,118,126,152.这组数据中,众数和中位数分别是( )
A.126,126 B.130,134 C.126,130 D.118,152
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com