
已知直角坐标系中有一点A(-4,3),点B在x轴上,△AOB是等腰三角形。
(1)求满足条件的所有点B的坐标。(直接写出答案)
(2)求过O、A、B三点且开口向下的抛物线的函数解析式。(只需求出满足条件的即可)。
(3)在(2)中求出的抛物线上存在点p,使得以O、A、B、P四点为顶点的四边形是梯形,求满足条件的所有点P的坐标及相应梯形的面积。

(1) (-5,0);(5,0);(-8,0);(-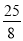 ,0).(2) 当AB=OA时,y=-
,0).(2) 当AB=OA时,y=-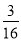 x2-
x2-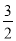 x;当OA=OB时,同理得y=-
x;当OA=OB时,同理得y=- x2-
x2-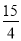 x;(3) (4,-9),48.(-12,-9),48. (1,-
x;(3) (4,-9),48.(-12,-9),48. (1,-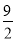 ),
), .(-9,-27),75.
.(-9,-27),75.
【解析】
试题分析:(1)根据点A的坐标,易求得OA=5,若△AOB是等腰三角形,应分三种情况考虑:
①OA=OB=5,由于点B的位置不确定,因此要分B在x轴正、负半轴两种情况求解,已知了OB的长,即可得到点B的坐标;
②OA=AB=5,此时点B只能在x轴负半轴上,那么点B的横坐标应为点A横坐标的2倍,可据此求得点B的坐标;
③AB=OB=5,此时点B只能在x轴负半轴上,可在x轴上截取AD=OA,通过构建相似三角形:△OBA∽△OAD,通过所得比例线段来求出OB的长,从而得到点B的坐标.
(2)任选一个(1)题所得的B点坐标,利用待定系数法求解即可.
(3)解此题时,虽然不同的抛物线有不同的解,但解法一致;分两种情况:
①OA∥BP时,可分别过A、P作x轴的垂线,设垂足为C、E,易证得△AOC∽△PBE,根据所得比例线段,即可求得点P的坐标.而梯形ABPO的面积可化为△ABO、△PBO的面积和来求出.
②OP∥AB时,方法同上,过P作PF⊥x轴于F,然后通过相似三角形:△ABC∽△POF,来求出P点坐标,梯形面积求法同上.(当OA=AB时,两种情况的点P正好关于抛物线对称轴对称,可据此直接求出P点坐标,避免重复计算.)
作AC⊥x轴,由已知得OC=4,AC=3,OA=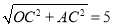
(1)当OA=OB=5时,
如果点B在x轴的负半轴上,如图(1),点B的坐标为(-5,0);
如果点B在x轴的正半轴上,如图(2),点B的坐标为(5,0);
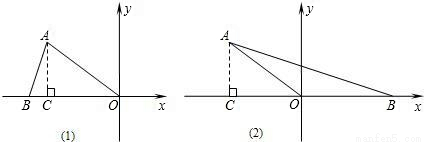
当OA=AB时,点B在x轴的负半轴上,如图(3),BC=OC,则OB=8,点B的坐标为(-8,0);
当AB=OB时,点B在x轴的负半轴上,如图(4),在x轴上取点D,使AD=OA,可知OD=8.
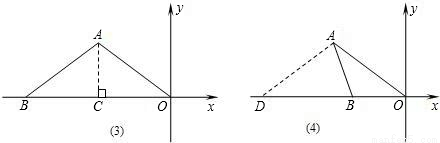
由∠AOB=∠OAB=∠ODA,可知△AOB∽△ODA,
则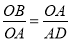 ,
,
解得OB=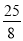 ,
,
点B的坐标为(-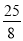 ,0).
,0).
(2)当AB=OA时,抛物线过O(0,0),A(-4,3),B(-8,0)三点,
设抛物线的函数表达式为y=ax2+bx,
可得方程组
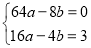 ,
,
解得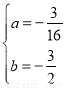 ,
,
∴y=-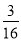 x2-
x2-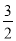 x;
x;
当OA=OB时,同理得y=- x2-
x2-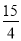 x;
x;
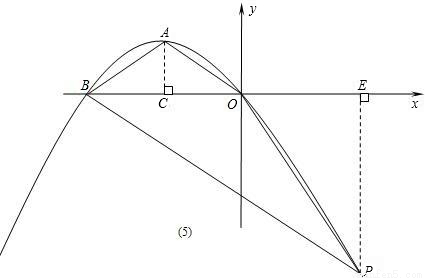
(3)当OA=AB时,若BP∥OA,如图(5),作PE⊥x轴,
则∠AOC=∠PBE,∠ACO=∠PEB=90°,
∴△AOC∽△PBE,
∴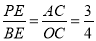 .
.
设BE=4m,PE=3m,则点P的坐标为(4m-8,-3m),
代入y=-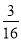 x2-
x2-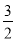 x,
x,
解得m=3;
则点P的坐标为(4,-9),
S梯形ABPO=S△ABO+S△BPO=48.
若OP∥AB,根据抛物线的对称性可得点P的坐标为(-12,-9),
S梯形AOPB=S△ABO+S△BPO=48.
当OA=OB时,若BP∥OA,如图(6),作PF⊥x轴,
则∠AOC=∠PBF,∠ACO=∠PFB=90°,
△AOC∽△PBF,
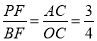 ;
;
设BF=4m,PF=3m,则点P的坐标为(4m-5,-3m),
代入y=-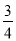 x2-
x2-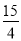 x,
x,
解得m=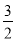 .则点P的坐标为(1,-
.则点P的坐标为(1,-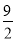 ),
),
S梯形ABPO=S△ABO+S△BPO= .
.
若OP∥AB(图略),作PF⊥x轴,
则∠ABC=∠POF,∠ACB=∠PFO=90°,
△ABC∽△POF,
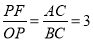 ;
;
设点P的坐标为(-n,-3n),
代入y=-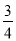 x2-
x2-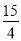 x,
x,
解得n=9.
则点P的坐标为(-9,-27),S梯形AOPB=S△ABO+S△BPO=75.
考点:二次函数综合题.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源:2013-2014学年安徽省当涂县四校九年级上学期期末联考数学试卷(解析版) 题型:选择题
如图所示的两个三角形是位似图形,它们的位似中心是

A.点O B.点P C.点M D.点N
查看答案和解析>>
科目:初中数学 来源:2013-2014学年安徽十大名校九年级第四次月考数学试卷(解析版) 题型:选择题
如图所示,已知AB∥CD,EF平分∠CEG,∠1=80°,则∠2的度数为

A.20° B.40° C.50° D.60°
查看答案和解析>>
科目:初中数学 来源:2013-2014学年四川省眉山市华兴联谊学校九年级下学期期中考试数学试卷(解析版) 题型:解答题
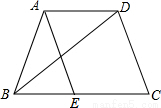
如图,在梯形ABCD中,AD∥BC,BD平分∠ABC,AE∥CD交BC于E,求证:AB=EC
查看答案和解析>>
科目:初中数学 来源:2013-2014学年四川省乐山市夹江县九年级毕业会考适应性考试数学试卷(解析版) 题型:解答题
如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的直线互相垂直,垂足为D,且AC平分∠DAB.
(1)求证:DC为⊙O的切线;
(2)若⊙O的半径为3,AD=4 ,求AC的长.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年吉林省长春市朝阳区中考一模数学试卷(解析版) 题型:选择题
如图,⊙O是△ABC的外接圆,连结OA、OB,且点C、O在弦AB的同侧,若∠ABO=50°,则∠ACB的度数为( )

A.50° B.45° C.30° D.40°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com