
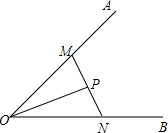
 已知:在∠AOB的边OA、OB上分别取M、N两点,使OM=ON;连接MN,取MN的中点P,连接OP,证明:射线OP是∠AOB的平分线.
已知:在∠AOB的边OA、OB上分别取M、N两点,使OM=ON;连接MN,取MN的中点P,连接OP,证明:射线OP是∠AOB的平分线.科目:初中数学 来源: 题型:
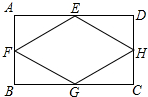 如图,E、F、G、H分别是矩形ABCD四边AB、BC、CD、AD的中点,
如图,E、F、G、H分别是矩形ABCD四边AB、BC、CD、AD的中点,查看答案和解析>>
科目:初中数学 来源: 题型:
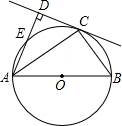 如图,C为以AB为直径的⊙O上一点,AD和过点C的切线互相垂直,垂足为点D.
如图,C为以AB为直径的⊙O上一点,AD和过点C的切线互相垂直,垂足为点D.查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 8 |
| 1 |
| 12 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 12 |
| 11 |
| 5 |
| 11 |
| 5 |
| 5 |
| 11 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
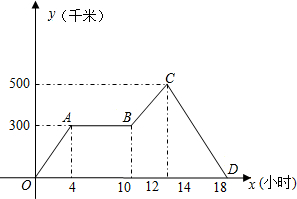 王老师从学校乘汽车去城里开会,4小时后,汽车出现故障,修理一段时间后继续走,又过了3个小时到达开会地点,而此时接到紧急通知,立马乘快客赶回学校.根据图中信息填空:
王老师从学校乘汽车去城里开会,4小时后,汽车出现故障,修理一段时间后继续走,又过了3个小时到达开会地点,而此时接到紧急通知,立马乘快客赶回学校.根据图中信息填空:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com