
【题目】为了了解江城中学学生的身高情况,随机对该校男生、女生的身高进行抽样调查,已知抽取的样本中,男生、女生的人数相同,根据所得数据绘制成如下所示的统计表和如图所示的统计图.

根据图表中提供的信息,回答下列问题:
(1)女生身高在B组的有________人;
(2)在样本中,身高在150≤x<155之间的共有________人,身高人数最多的在________组(填组别序号);
(3)已知该校共有男生500人,女生480人,请估计身高在155≤x<165之间的学生有多少人.
【答案】(1)12;(2)16;C;(3)541人.
【解析】试题分析:对于(1),如图所示,男生身高在各组的人数分别为2、4、12、14、8,共有40人;
由扇形统计图易得女生身高在B组的所占百分比为30%,女生人数和男生人数一样,共40人,用40乘以30%即可求出女生身高在B组的人数;
对于(2),由图可知,身高在150≤x<155之间的男生有4人,女生有12人,将二者相加即可得到身高在150≤x<155之间的人数;
由扇形统计图可知女生身高在各组的人数分别为8、12、12、6、2,将男女生身高在各组的人数加起来即可得男女生身高在各组的总人数为10、16、24、20、10,据此可得到身高人数最多的在哪个组;
对于(3),先根据图表分别求出男女生身高在155≤x<165之间的人数比例,再由样本估计总体分别乘以该校男女生人数,相加即可求出该校学生身高在155≤x<165之间的学生人数.
解:(1)由条形统计图可知男生身高在各组的人数分别为2、4、12、14、8,共有2+4+8+12+14=40(人),
又因为男生和女生的人数相同,
所以女生身高在B组的人数有40×(1-30%-20%-15%-5%)=12(人).
(2)在样本中,身高在150≤x<155之间的人数共有4+12=16(人),
女生身高在各组的人数分别为8、12、12、6、2人,男生身高在各组的人数分别为2、4、12、14、8人,将男女生身高在各组的人数加起来即可得男女生身高在各组的总人数为10、16、24、20、10,所以身高人数最多的在C组.
(3)500×![]() +480×(30%+15%)=541(人),
+480×(30%+15%)=541(人),
所以估计身高在155≤x<165之间的学生有541人.


科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示.A(2,3),B(3,1),C(﹣2,﹣2)三点在格点上.

(1)作出△ABC关于y轴对称的△A1B1C1;
(2)直接写出△ABC关于x轴对称的△A2B2C2的各点坐标;
(3)求出△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列多项式相乘,可以用平方差公式直接计算的是( )
A.(x+5y)(x-5y)B.(-3x+4y)(4y-3x)
C.(x+3y)(2x-3y)D.(3x-2y)(2y-3x)
查看答案和解析>>
科目:初中数学 来源: 题型:
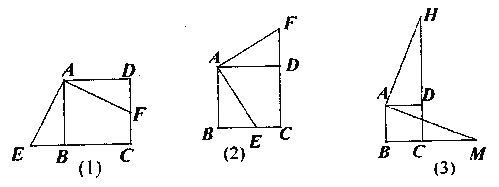
【题目】(1)观察发现:四边形ABCD是正方形,点E是直线BC上的动点,连结AE,过点A作AF⊥AE交直线CD于F.当点E位于点B的左侧时,如图(1).观察线段AB.BE.CF之间有何数量关系?请直接写出线段AB.BE.CF之间的数量关系.
(2)拓展探究:当点E位于点B的右侧时,如图(2),线段AB.BE.CF之间有何数量关系?并说明理由.
(3)迁移应用:如图(3),正方形ABCD的边长为2cm时,线段CM=3cm,直接写出线段CH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
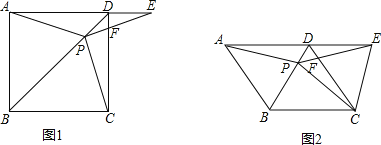
【题目】如图1在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120度时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD,AB=AC,点E,F分别是BC,AD的中点,连接AE,CF.
(1)求证:四边形AECF是矩形;
(2)若AB=8,求菱形的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明爸爸经营的水果店出售一种优质热带水果,正在上初三的小明经过调查和计算,发现这种水果每月的销售量y(千克)与销售单价x(元)之间存在着一次函数关系:y=-10x+500(20≤x≤50).下面是他们的一次对话:
小明:“您要是告诉我咱家这种水果的进价是多少?我就能帮你预测好多信息呢!”
爸爸:“咱家这种水果的进价是每千克20元”
聪明的你,也来解答一下小明想要解决的两个问题:
(1)若每月获得利润w(元)是销售单价x(元)的函数,求这个函数的表达式.
(2)当销售单价为多少元时,每月可获得最大利润?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com