
【题目】中秋佳节我国有赏月和吃月饼的传统,英才学校数学兴趣小组为了了解本校学生喜爱月饼的情况,随机抽取了60名同学进行问卷调查,经过统计后绘制了两幅尚不完整的统计图.(注:参与问卷调查的每一位同学在任何一种分类统计中只有一种选择)请根据统计图完成下列问题:
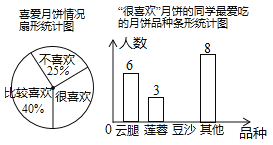
(1)扇形统计图中,“很喜欢”的部分所对应的圆心角为 度;条形统计图中,“很喜欢”月饼中喜欢“豆沙”月饼的学生有 人;
(2)若该校共有学生1200人,请根据上述调查结果,估计该校学生中“很喜欢”月饼的有 人.
(3)李民同学最爱吃莲蓉月饼,陈丽同学最爱吃豆沙月饼,现有重量、包装完全一样的豆沙、莲蓉、蛋黄
三种月饼各一个,让李民、陈丽每人各选一个,则李民、陈丽两人都选中自己最爱吃的月饼的概率为 .
【答案】(1)126°,4;(2)675;(3)![]() .
.
【解析】试题分析:(1)根据“很喜欢”的部分占的百分比,计算所对应的圆心角;
(2)用样本估计总体的思想即可解决问题.
(3)画出树状图,根据概率的定义即可解决.
试题解析:(1)∵“很喜欢”的部分占的百分比为:1﹣25%﹣40%=35%,∴扇形统计图中,“很喜欢”的部分所对应的圆心角为:360°×35%=126°;
∵“很喜欢”月饼的同学数:60×35%=21,∴条形统计图中,喜欢“豆沙”月饼的学生数:21﹣6﹣3﹣8=4,故答案分别为126°,4.
(2)900名学生中“很喜欢”的有900×35%=315人,900名学生中“比较喜欢”的有900×40%=360人,∴估计该校学生中“很喜欢”和“比较喜欢”月饼的共有675人.
故答案为:675.
(3)无聊表示方便,记云腿、豆沙、莲蓉、蛋黄四种月饼分别为A、B、C、D.画出的树状图如图所示,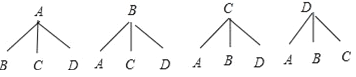
∴甲、乙两人中有且只有一人选中自己最爱吃的月饼的概率=![]() =
=![]()


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过A(﹣3.0)、C(0,4),点B在抛物线上,CB∥x轴,且AB平分∠CAO.
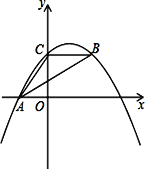
(1)求抛物线的解析式a,b,c;
(2)线段AB上有一动点P,过点P作y轴的平行线,交抛物线于点Q,求线段PQ的最大值;
(3)抛物线的对称轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在求出点M坐标;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列 ![]() 个命题:其中真命题是( ).
个命题:其中真命题是( ).
⑴三角形的外角和是 ![]() ;⑵三角形的三个内角中至少有两个锐角;⑶直角三角形两锐角互余;⑷相等的角是对顶角.
;⑵三角形的三个内角中至少有两个锐角;⑶直角三角形两锐角互余;⑷相等的角是对顶角.
A.( ![]() )(
)( ![]() )
)
B.( ![]() )(
)( ![]() )
)
C.( ![]() )(
)( ![]() )
)
D.( ![]() )(
)( ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级教材在图形与几何部分给出了五条基本事实,在《证明》一章中我们从两条基本事实出发,把前面得到的平行线相关性质进行了严格的证明,体会了数学的公里化思想.请完成下列证明活动:
(1)活动 ![]() .利用基本事实证明:“两直线平行,同位角相等”.(在括号内填上相应的基本事实)
.利用基本事实证明:“两直线平行,同位角相等”.(在括号内填上相应的基本事实)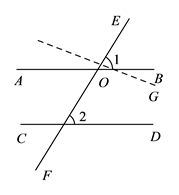
已知:如图,直线 ![]() 、
、 ![]() 被直线
被直线 ![]() 所截,
所截, ![]() .
.
求证: ![]() .
.
证明:假设 ![]() ,则可以过点
,则可以过点 ![]() 作
作 ![]() .
.
∵ ![]() ,
,
∴ ![]() ().
().
∴过 ![]() 点存在两条直线
点存在两条直线 ![]() 、
、 ![]() 两条直线与
两条直线与 ![]() 平行,这与基本事实()矛盾.
平行,这与基本事实()矛盾.
∴假设不成立.
∴ ![]() .
.
(2)活动 ![]() .利用刚刚证明的“两直线平行,同位角相等”证明“两直线平行,同旁内角互补”.(要求画图,写出已知、求证并写出证明过程)
.利用刚刚证明的“两直线平行,同位角相等”证明“两直线平行,同旁内角互补”.(要求画图,写出已知、求证并写出证明过程)
已知:.
求证:.
证明: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知坐标平面内的点A(-2,5),若将平面直角坐标系先向右平移3个单位长度,再向上平移4个单位长度,则点A在平移后的坐标系中的坐标是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知抛物线y=x2+bx+c与x轴交于A、B两点(点A在点B左侧),与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.
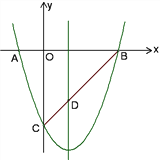
(1)求抛物线的函数表达式;
(2)求直线BC的函数表达式;
(3)点E为y轴上一动点,CE的垂直平分线交CE于点F,交抛物线于P、Q两点,且点P在第三象限.
①当线段PQ ![]() 时,求tan∠CED的值;
时,求tan∠CED的值;
②当以C、D、E为顶点的三角形是直角三角形时,请直接写出点P的坐标.
(参考公式:抛物线![]() 的顶点坐标是
的顶点坐标是 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com