
【题目】已知点D与点A(0,6),B(0,﹣4),C(x,y)是平行四边形的四个顶点,其中x,y满足x﹣y+3=0,则CD长的最小值为( )
A.![]()
B.4
C.2
D.2 ![]()
【答案】D
【解析】解:根据平行四边形的性质可知:对角线AB、CD互相平分,
∴CD过线段AB的中点M,即CM=DM,
∵A(0,6),B(0,﹣4),
∴M(0,1),
∵点到直线的距离垂线段最短,
∴过M作直线的垂线交直线于点C,此时CM最小,
直线x﹣y+3=0,令x=0得到y=3;令y=0得到x=﹣3,即F(﹣3,0),E(0,3),
∴OE=3,OF=3,EM=2,EF= ![]() =3
=3 ![]() ,
,
∵△EOF∽△ECM,
∴ ![]() ,
,
即 ![]() ,
,
解得:CM= ![]() ,
,
则CD的最小值为2CM=2 ![]() .
.
故选D.
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A(3,4),B(5,0),C(0,﹣2).在第一象限找一点D,使四边形AOBD成为平行四边形,
(1)点D的坐标是;
(2)连接OD,线段OD、AB的关系是;
(3)若点P在线段OD上,且使PC+PB最小,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点F,C是⊙O上两点,且![]() ,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.

(1)求证:CD是⊙O的切线;
(2)若CD=2![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的边OA在x轴正半轴上,边OC在y轴正半轴上,B点的坐标为(1,3).矩形O′A′BC′是矩形OABC绕B点逆时针旋转得到的.O′点恰好在x轴的正半轴上,O′C′交AB于点D.
(1)求点O′的坐标,并判断△O′DB的形状(要说明理由)
(2)求边C′O′所在直线的解析式.
(3)延长BA到M使AM=1,在(2)中求得的直线上是否存在点P,使得△POM是以线段OM为直角边的直角三角形?若存在,请直接写出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ADF≌△CBE,且点E,B,D,F在一条直线上.试判断:
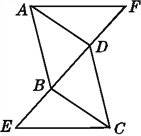
(1)AD与BC的位置关系(并加以说明);
(2)BF与DE的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息汇集如下:
如图,AB∥OH∥CD,相邻两平行线间的距离相等,AC,BD相交于O,OD⊥CD.垂足为D,已知AB=20米,请根据上述信息求标语CD的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明想知道湖中两个小亭A、B之间的距离,他在与小亭A、B位于同一水平面且东西走向的湖边小道![]() 上某一观测点M处,测得亭A在点M的北偏东30°方向, 亭B在点M的北偏东60°方向,当小明由点M沿小道
上某一观测点M处,测得亭A在点M的北偏东30°方向, 亭B在点M的北偏东60°方向,当小明由点M沿小道![]() 向东走60米时,到达点N处,此时测得亭A恰好位于点N的正北方向,继续向东走30米时到达点Q处,此时亭B恰好位于点Q的正北方向,根据以上测量数据,请你帮助小明计算湖中两个小亭A、B之间的距离.
向东走60米时,到达点N处,此时测得亭A恰好位于点N的正北方向,继续向东走30米时到达点Q处,此时亭B恰好位于点Q的正北方向,根据以上测量数据,请你帮助小明计算湖中两个小亭A、B之间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
(1)作出△ABC绕点A逆时针旋转90°的△AB1C1 , 再作出△AB1C1关于原点O成中心对称的△A1B2C2 .
(2)点B1的坐标为 , 点C2的坐标为 .
(3)△ABC经过怎样的旋转可直接得到△A1B2C2 , .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com