
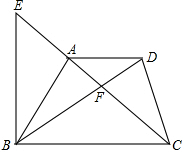
 如图,在梯形ABCD中,AD∥BC,AC与BD相交于点F,E是对角线CA延长线上的一点,且FC2=FA•FE,求证:BE∥CD.
如图,在梯形ABCD中,AD∥BC,AC与BD相交于点F,E是对角线CA延长线上的一点,且FC2=FA•FE,求证:BE∥CD. 分析 根据相似三角形的判定,由AD∥BC可判断△FAD∽△FCB,则根据相似三角形的性质得$\frac{FA}{FC}$=$\frac{FD}{FB}$,再根据比例的性质,由FC2=FA•FE得到$\frac{FA}{FC}$=$\frac{FC}{FE}$,所以$\frac{FD}{FB}$=$\frac{FC}{FE}$,加上∠DFC=∠BFE,则根据相似三角形的判定可得△FDC∽△FBC,则∠FCD=∠E,然后根据平行线的判定方法得BE∥CD.
解答 证明:∵AD∥BC,
∴△FAD∽△FCB,
∴$\frac{FA}{FC}$=$\frac{FD}{FB}$,
∵FC2=FA•FE,
∴$\frac{FA}{FC}$=$\frac{FC}{FE}$,
∴$\frac{FD}{FB}$=$\frac{FC}{FE}$,
而∠DFC=∠BFE,
∴△FDC∽△FBC,
∴∠FCD=∠E,
∴BE∥CD.
点评 本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;在利用三角形相似的性质时,注意对应角相等.也考查了梯形的性质.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
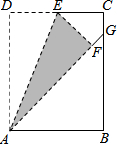 如图,在矩形ABCD中,AB=4,AD=2$\sqrt{5}$,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部.将AF延长交边BC于点G.则 $\frac{CG}{GB}$=$\frac{1}{5}$.
如图,在矩形ABCD中,AB=4,AD=2$\sqrt{5}$,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部.将AF延长交边BC于点G.则 $\frac{CG}{GB}$=$\frac{1}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
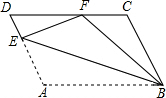 如图,在?ABCD中,E为AD上一点,以BE为折痕将△ABE向上翻折,点A恰好落在CD上的点F处.若△FDE的周长为12,△FCB的周长为22,则FC的长为5.
如图,在?ABCD中,E为AD上一点,以BE为折痕将△ABE向上翻折,点A恰好落在CD上的点F处.若△FDE的周长为12,△FCB的周长为22,则FC的长为5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com