
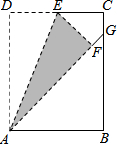
 如图,在矩形ABCD中,AB=4,AD=2$\sqrt{5}$,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部.将AF延长交边BC于点G.则 $\frac{CG}{GB}$=$\frac{1}{5}$.
如图,在矩形ABCD中,AB=4,AD=2$\sqrt{5}$,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部.将AF延长交边BC于点G.则 $\frac{CG}{GB}$=$\frac{1}{5}$. 分析 如图,作辅助线,首先证明△EFG≌△ECG,得到FG=CG(设为x ),∠FEG=∠CEG;同理可证AF=AD=2$\sqrt{5}$,∠FEA=∠DEA,进而证明△AEG为直角三角形,运用射影定理即可解决问题.
解答 解:如图: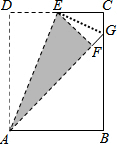
连接EG;
∵四边形ABCD为矩形,
∴∠D=∠C=90°,DC=AB=4;
由题意得:EF=DE=EC=2,∠EFG=∠D=90°;
在Rt△EFG与Rt△ECG中,
$\left\{\begin{array}{l}{EF=EC}\\{EG=EG}\end{array}\right.$,
∴△EFG≌△ECG,
∴FG=CG(设为x ),∠FEG=∠CEG;
同理可证:AF=AD=2$\sqrt{5}$,∠FEA=∠DEA,
∴∠AEG=$\frac{1}{2}$×180°=90°,而EF⊥AG,由射影定理得:
22=2$\sqrt{5}$•x,
∴x=$\frac{2}{5}$$\sqrt{5}$,
∴$\frac{CG}{GB}$=$\frac{1}{5}$.
故答案为:$\frac{1}{5}$.
点评 此题考查矩形的性质,翻折变换的性质,以考查全等三角形的性质及其应用、射影定理等几何知识点为核心构造而成;对综合的分析问题解决问题的能力提出了一定的要求.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
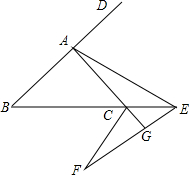 如图,在△ABC中,∠B=45°,点D为BA延长线上一点,作∠DAE=∠BAC,交BC延长交于点E,将△ACE沿CE所在直线折叠压平,得到△FCE,延长AC交EF于点G,探究AG与EF的位置关系,并说明理由.
如图,在△ABC中,∠B=45°,点D为BA延长线上一点,作∠DAE=∠BAC,交BC延长交于点E,将△ACE沿CE所在直线折叠压平,得到△FCE,延长AC交EF于点G,探究AG与EF的位置关系,并说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com