
已知:二次函数 (m为常数).
(m为常数).
(1)若这个二次函数的图象与x轴只有一个公共点A,且A点在x轴的正半轴上.
①求m的值;
②四边形AOBC是正方形,且点B在y轴的负半轴上,现将这个二次函数的图象平移,使平移后的函数图象恰好经过B,C两点,求平移后的图象对应的函数解析式;
(2)当0≤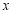 ≤2时,求函数
≤2时,求函数 的最小值(用含m的代数式表示).
的最小值(用含m的代数式表示).

(1)m=4; y=x2-2x-2.(2)当m<0时,函数y=x2-mx+ m+1的最小值为
m+1的最小值为 m+1;当0≤m≤4时,函数y=x2-mx+
m+1;当0≤m≤4时,函数y=x2-mx+ m+1的最小值为-
m+1的最小值为-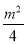 +
+ m+1;当m>4时,函数y=x2-mx+
m+1;当m>4时,函数y=x2-mx+ m+1的最小值为-
m+1的最小值为- m+5.
m+5.
【解析】
试题分析:(1)①根据二次函数x2-mx+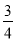 m+1的图象与x轴只有一个公共点A,可得判别式为0,依此可得关于m的方程,求解即可;
m+1的图象与x轴只有一个公共点A,可得判别式为0,依此可得关于m的方程,求解即可;
②由①得点A的坐标为(2,0).根据正方形的性质可得点B的坐标为(0,-2),点C的坐标为(2,-2).根据待定系数法可求平移后的图象对应的函数解析式;
(2)分三种情况:(ⅰ)当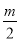 <0,即m<0时;(ⅱ)当0≤
<0,即m<0时;(ⅱ)当0≤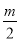 ≤2,即0≤m≤4时;(ⅲ)当
≤2,即0≤m≤4时;(ⅲ)当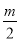 >2,即m>4时;讨论可求函数y=x2-mx+
>2,即m>4时;讨论可求函数y=x2-mx+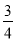 m+1的最小值.
m+1的最小值.
试题解析:(1)①∵二次函数y=x2-mx+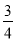 m+1的图象与x轴只有一个公共点A,
m+1的图象与x轴只有一个公共点A,
∴△=m2-4×1×(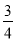 m+1)=0.
m+1)=0.
整理,得m2-3m-4=0,
解得m1=4,m2=-1,
又∵点A在x轴的正半轴上,
∴m=4.
②由①得点A的坐标为(2,0).
∵四边形AOBC是正方形,点B在y轴的负半轴上,
∴点B的坐标为(0,-2),点C的坐标为(2,-2).
设平移后的图象对应的函数解析式为y=x2+bx+c(b,c为常数).
∴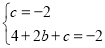 ,
,
解得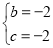
∴平移后的图象对应的函数解析式为y=x2-2x-2.
(2)函数y=x2-mx+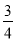 m+1的图象是顶点为(
m+1的图象是顶点为(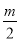 ,-
,-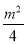 +
+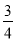 m+1),且开口向上的抛物线.分三种情况:
m+1),且开口向上的抛物线.分三种情况:
(ⅰ)当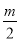 <0,即m<0时,函数在0≤x≤2内y随x的增大而增大,此时函数的最小值为
<0,即m<0时,函数在0≤x≤2内y随x的增大而增大,此时函数的最小值为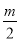 m+1;
m+1;
(ⅱ)当0≤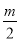 ≤2,即0≤m≤4时,函数的最小值为-
≤2,即0≤m≤4时,函数的最小值为-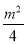 +
+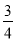 m+1;
m+1;
(ⅲ)当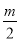 >2,即m>4时,函数在0≤x≤2内y随x的增大而减小,此时函数的最小值为-
>2,即m>4时,函数在0≤x≤2内y随x的增大而减小,此时函数的最小值为-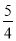 m+5.
m+5.
综上所述,当m<0时,函数y=x2-mx+ m+1的最小值为
m+1的最小值为 m+1;当0≤m≤4时,函数y=x2-mx+
m+1;当0≤m≤4时,函数y=x2-mx+ m+1的最小值为-
m+1的最小值为-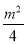 +
+ m+1;当m>4时,函数y=x2-mx+
m+1;当m>4时,函数y=x2-mx+ m+1的最小值为-
m+1的最小值为- m+5.
m+5.
考点:二次函数综合题.


科目:初中数学 来源:2014-2015学年江苏省启东市八年级上学期期中考试数学试卷(解析版) 题型:选择题
如图是由九个等边三角形组成的一个六边形,当最小的等边三角形边长为2cm时,这个六边形的周长为( )cm.

A.30 B.40 C.50 D.60
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省启东市八年级上学期期中考试数学试卷(解析版) 题型:选择题
在平面直角坐标系中,点A(-1,2)关于x轴对称的点B的坐标为( )
A.(-1,2) B.(1,2) C.(1,-2) D.(-1,-2)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省启东市九年级上学期期中考试数学试卷(解析版) 题型:解答题
如图,用长为20米的篱笆恰好围成一个扇形花坛,且扇形花坛的圆心角小于180°,设扇形花坛的半径为r米,面积为S平方米.(注: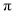 的近似值取3)
的近似值取3)
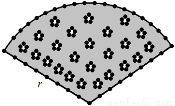
(1)求出S与r的函数关系式,并写出自变量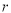 的取值范围;
的取值范围;
(2)当半径r为何值时,扇形花坛的面积最大,并求面积的最大值.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省启东市九年级上学期期中考试数学试卷(解析版) 题型:填空题
如图,在△ABC中,∠ACB=90°,∠ABC=30°,BC=2.将△ABC绕点C逆时针旋转 角后得到△A′B′C,当点A的对应点A' 落在AB边上时,旋转角
角后得到△A′B′C,当点A的对应点A' 落在AB边上时,旋转角 的度数是 度,阴影部分的面积为 .
的度数是 度,阴影部分的面积为 .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省启东市九年级上学期第一次单元测试数学试卷(解析版) 题型:解答题
已知二次函数的图象的一部分如图所示,求:

(1)这个二次函数关系式,
(2)求图象与x轴的另一个交点,
(3)看图回答,当x取何值时y ﹤0.(12分)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省南通市海安县八年级上学期期中考试数学试卷(解析版) 题型:选择题
如图,∠BAC与∠CBE的平分线相交于点P,BE=BC,PB与CE交于点H,PG∥AD交BC于F,交AB于G,下列结论:①GA=GP;② ;③BP垂直平分CE;④FP=FC;其中正确的判断有( )
;③BP垂直平分CE;④FP=FC;其中正确的判断有( )

A.只有①② B.只有③④ C.只有①③④ D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com