练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    8．如图△ABC中，∠D=90°，C是BD上一点，已知CB=9，AB=17，AC=10，则DC的长是6，AD=8．

    分析 先设CD=x，则BD=BC+CD=9+x，再运用勾股定理分别在△ACD与△ABD中表示出AD2，列出方程，求解即可．

    解答 解：设CD=x，则BD=BC+CD=9+x．
    在△ACD中，∵∠D=90°，
    ∴AD2=AC2-CD2，
    在△ABD中，∵∠D=90°，
    ∴AD2=AB2-BD2，
    ∴AC2-CD2=AB2-BD2，
    即102-x2=172-（9+x）2，
    解得：x=6，即CD=6，
    ∴AD2=102-62=64，
    ∴AD=8．
    故答案为：6，8．

    点评 本题主要考查了勾股定理的运用，根据AD的长度不变列出方程是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    10．某班共有a名学生，其中男生人数占40%，那么女生人数为（　　）
    A．40%aB．（1-40%）aC．$\frac{a}{40%}$D．$\frac{a}{1-40%}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．有下列说法：①一个有理数不是整数就是分数；②一个有理数不是正数就是负数；③一个整数不是正的，就是负的；④一个分数不是正的，就是负的；⑤若ab=1，则a与b互为倒数；⑥|a|＞|b|且a，b异号，则a+b＞0；其中说法正确的有（　　）
    A．5个B．4个C．3个D．2个

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

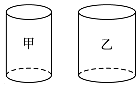    16．如图，在水平桌面上有甲、乙两个内部呈圆柱形的容器，内部底面积分别为80cm 2、100cm 2，且甲容器装满水，乙容器是空的．若将甲中的水全部倒入乙中，则乙中的水位高度比原先甲的水位高度低了8cm，则甲的容积是（　　）
    A．1280 cm 3B．2560 cm 3C．3200 cm 3D．4000 cm 3

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．在Rt△ABC，∠C=90°，AC=4cm，BC=3cm，D为AB边的中点，则CD=2.5cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．我们知道：分式和分数有着很多的相似点，如类比分数的基本性质，我们得到了分式的基本性质：类比分数的运算法则，我们得到了分式的运算法则，等等．小学里，把分子比分母小的分数叫做真分数．类似地，我们把分子整式的次数小于分母整式的次数的分式称为真分式；反之，称为假分式，对于任何一个假分式都可以化成整式与真分式的和的形式．
    如：$\frac{x+1}{x-1}$=$\frac{x-1+2}{x-1}$=$\frac{x-1}{x-1}$+$\frac{2}{x-1}$=1+$\frac{2}{x-1}$；
    $\frac{2x-3}{x+1}$=$\frac{2x+2-5}{x+1}$=$\frac{2x+2}{x+1}$+$\frac{-5}{x+1}$=2+（-$\frac{5}{x+1}$）．
    （1）下列分式中：①$\frac{x-1}{x+1}$，②$\frac{{x}^{2}}{x-1}$，③$\frac{4y}{2{y}^{2}+1}$，④$\frac{{m}^{2}+3}{{m}^{2}-1}$，属于真分式的是③（填序号）；
    （2）将假分式$\frac{4a+5}{2a-1}$化成整式与真分式的和的形式为：
    $\frac{4a+5}{2a-1}$=2+$\frac{7}{2a-1}$，若假分式$\frac{4a+5}{2a-1}$的值为整数，则整数a的值为1或0或4或-3；
    （3）将假分式$\frac{{a}^{2}-3}{a+1}$化成整式与真分式的和的形式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

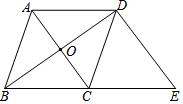    20．如图，在菱形ABCD中，对角线AC、BD相交于点O，且AB=5，AC=6，过点D作AC的平行线交BC的延长线于点E，则△BDE的面积为24．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

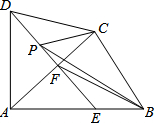    17．如图四边形ABCD中，AD=DC，∠DAB=∠ACB=90°，过点D作DF⊥AC，垂足为F．DF与AB相交于E．设AB=15，BC=9，P是射线DF上的动点．当△BCP的周长最小时，DP的长为12.5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．先化简，再求值：$（{\frac{1}{x-2}-1}）÷\frac{{{x^2}-3x}}{{{x^2}-4x+4}}$，其中x=$\sqrt{2}$+1．

    查看答案和解析>>

    同步练习册答案