
【题目】如图,将函数y= ![]() (x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )
(x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( ) 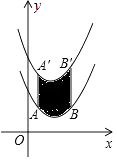
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】解:∵函数y= ![]() (x﹣2)2+1的图象过点A(1,m),B(4,n), ∴m=
(x﹣2)2+1的图象过点A(1,m),B(4,n), ∴m= ![]() (1﹣2)2+1=1
(1﹣2)2+1=1 ![]() ,n=
,n= ![]() (4﹣2)2+1=3,
(4﹣2)2+1=3,
∴A(1,1 ![]() ),B(4,3),
),B(4,3),
过A作AC∥x轴,交B′B的延长线于点C,则C(4,1 ![]() ),
),
∴AC=4﹣1=3,
∵曲线段AB扫过的面积为9(图中的阴影部分),
∴ACAA′=3AA′=9,
∴AA′=3,
即将函数y= ![]() (x﹣2)2+1的图象沿y轴向上平移3个单位长度得到一条新函数的图象,
(x﹣2)2+1的图象沿y轴向上平移3个单位长度得到一条新函数的图象,
∴新图象的函数表达式是y= ![]() (x﹣2)2+4.
(x﹣2)2+4.
故选D.
【考点精析】根据题目的已知条件,利用二次函数图象的平移的相关知识可以得到问题的答案,需要掌握平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知直线l:y=﹣x﹣1,双曲线y= ![]() ,在l上取一点A1 , 过A1作x轴的垂线交双曲线于点B1 , 过B1作y轴的垂线交l于点A2 , 请继续操作并探究:过A2作x轴的垂线交双曲线于点B2 , 过B2作y轴的垂线交l于点A3 , …,这样依次得到l上的点A1 , A2 , A3 , …,An , …记点An的横坐标为an , 若a1=2,则a2= , a2013=;若要将上述操作无限次地进行下去,则a1不可能取的值是 .
,在l上取一点A1 , 过A1作x轴的垂线交双曲线于点B1 , 过B1作y轴的垂线交l于点A2 , 请继续操作并探究:过A2作x轴的垂线交双曲线于点B2 , 过B2作y轴的垂线交l于点A3 , …,这样依次得到l上的点A1 , A2 , A3 , …,An , …记点An的横坐标为an , 若a1=2,则a2= , a2013=;若要将上述操作无限次地进行下去,则a1不可能取的值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场进了一批家用空气净化器,成本为1200元/台.经调查发现,这种空气净化器每周的销售量y(台)与售价x(元/台)之间的关系如图所示: 
(1)请写出这种空气净化器每周的销售量y与 售价x的函数关系式(不写自变量的范围);
(2)若空气净化器每周的销售利润为W(元),则当售价为多少时,可获得最大利润,此时的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BA=AE=DC,AD=EC,CE⊥AE,垂足为E. 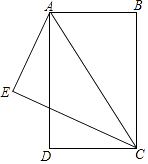
(1)求证:△DCA≌△EAC;
(2)只需添加一个条件,即 , 可使四边形ABCD为矩形.请加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店在2014年至2016年期间销售一种礼盒.2014年,该商店用3500元购进了这种礼盒并且全部售完;2016年,这种礼盒的进价比2014年下降了11元/盒,该商店用2400元购进了与2014年相同数量的礼盒也全部售完,礼盒的售价均为60元/盒.
(1)2014年这种礼盒的进价是多少元/盒?
(2)若该商店每年销售这种礼盒所获利润的年增长率相同,问年增长率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把多块大小不同的30°直角三角板如图所示,摆放在平面直角坐标系中,第一块三角板AOB的一条直角边与y轴重合且点A的坐标为(0,1),∠ABO=30°;第二块三角板的斜边BB1与第一块三角板的斜边AB垂直且交y轴于点B1;第三块三角板的斜边B1B2与第二块三角板的斜边BB1垂直且交x轴于点B2;第四块三角板的斜边B2B3与第三块三角板的斜边B1B2C垂直且交y轴于点B3;…按此规律继续下去,则点B2017的坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE. 
(1)求证:BE与⊙O相切;
(2)设OE交⊙O于点F,若DF=1,BC=2 ![]() ,求阴影部分的面积.
,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下说法: ①关于x的方程x+ ![]() =c+
=c+ ![]() 的解是x=c(c≠0);
的解是x=c(c≠0);
②方程组 ![]() 的正整数解有2组;
的正整数解有2组;
③已知关于x,y的方程组 ![]() ,其中﹣3≤a≤1,当a=1时,方程组的解也是方程x+y=4﹣a的解;
,其中﹣3≤a≤1,当a=1时,方程组的解也是方程x+y=4﹣a的解;
其中正确的有( )
A.②③
B.①②
C.①③
D.①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com