
【题目】以下说法: ①关于x的方程x+ ![]() =c+
=c+ ![]() 的解是x=c(c≠0);
的解是x=c(c≠0);
②方程组 ![]() 的正整数解有2组;
的正整数解有2组;
③已知关于x,y的方程组 ![]() ,其中﹣3≤a≤1,当a=1时,方程组的解也是方程x+y=4﹣a的解;
,其中﹣3≤a≤1,当a=1时,方程组的解也是方程x+y=4﹣a的解;
其中正确的有( )
A.②③
B.①②
C.①③
D.①②③
【答案】A
【解析】解:①关于x的方程x+ ![]() =c+
=c+ ![]() 的解是x=c或x=
的解是x=c或x= ![]() (c≠0),故此选项错误; ②方程组
(c≠0),故此选项错误; ②方程组 ![]() 的正整数解有2组,
的正整数解有2组,
方程组 ![]() ,
,
∵x、y、z是正整数,
∴x+y≥2
∵23只能分解为23×1
方程②变为(x+y)z=23
∴只能是z=1,x+y=23
将z=1代入原方程转化为 ![]() ,
,
解得x=2、y=21或x=20、y=3
∴这个方程组的正整数解是(2,21,1)、(20,3,1),故此选项正确;
③关于x,y的方程组 ![]() ,其中﹣3≤a≤1,解得x=1+2a,y=1﹣a,x+y=2+a,
,其中﹣3≤a≤1,解得x=1+2a,y=1﹣a,x+y=2+a,
当a=1时,x+y=3,故方程组的解也是方程x+y=4﹣a=3的解,此选项正确.
故选:A.
【考点精析】通过灵活运用二元一次方程组的解和分式方程的解,掌握二元一次方程组中各个方程的公共解,叫做这个二元一次方程的解;分式方程无解(转化成整式方程来解,产生了增根;转化的整式方程无解);解的正负情况:先化为整式方程,求整式方程的解即可以解答此题.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,将函数y= ![]() (x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )
(x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( ) 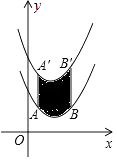
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转运甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止). 
(1)请用列表或画树状图的方法表示出上述游戏中两数和的所有可能的结果;
(2)分别求出李燕和刘凯获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】天水某公交公司将淘汰某一条线路上“冒黑烟”较严重的公交车,计划购买A型和B型两行环保节能公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元,
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在该条线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1220万元,且确保这10辆公交车在该线路的年均载客量总和不少于650万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下说法: ①关于x的方程x+ ![]() =c+
=c+ ![]() 的解是x=c(c≠0);
的解是x=c(c≠0);
②方程组 ![]() 的正整数解有2组;
的正整数解有2组;
③已知关于x,y的方程组 ![]() ,其中﹣3≤a≤1,当a=1时,方程组的解也是方程x+y=4﹣a的解;
,其中﹣3≤a≤1,当a=1时,方程组的解也是方程x+y=4﹣a的解;
其中正确的有( )
A.②③
B.①②
C.①③
D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,双曲线y= ![]() (x>0)与直线EF交于点A,点B,且AE=AB=BF,连结AO,BO,它们分别与双曲线y=
(x>0)与直线EF交于点A,点B,且AE=AB=BF,连结AO,BO,它们分别与双曲线y= ![]() (x>0)交于点C,点D,则:
(x>0)交于点C,点D,则:
(1)①AB与CD的位置关系是;
②四边形ABDC的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=3ax2+2bx+c
(1)若a=b=1,c=﹣1求该抛物线与x轴的交点坐标;
(2)若a= ![]() ,c=2+b且抛物线在﹣2≤x≤2区间上的最小值是﹣3,求b的值;
,c=2+b且抛物线在﹣2≤x≤2区间上的最小值是﹣3,求b的值;
(3)若a+b+c=1,是否存在实数x,使得相应的y的值为1,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com