
【题目】以下说法: ①关于x的方程x+ ![]() =c+
=c+ ![]() 的解是x=c(c≠0);
的解是x=c(c≠0);
②方程组 ![]() 的正整数解有2组;
的正整数解有2组;
③已知关于x,y的方程组 ![]() ,其中﹣3≤a≤1,当a=1时,方程组的解也是方程x+y=4﹣a的解;
,其中﹣3≤a≤1,当a=1时,方程组的解也是方程x+y=4﹣a的解;
其中正确的有( )
A.②③
B.①②
C.①③
D.①②③
【答案】A
【解析】解:①关于x的方程x+ ![]() =c+
=c+ ![]() 的解是x=c或x=
的解是x=c或x= ![]() (c≠0),故此选项错误; ②方程组
(c≠0),故此选项错误; ②方程组 ![]() 的正整数解有2组,
的正整数解有2组,
方程组 ![]() ,
,
∵x、y、z是正整数,
∴x+y≥2
∵23只能分解为23×1
方程②变为(x+y)z=23
∴只能是z=1,x+y=23
将z=1代入原方程转化为 ![]() ,
,
解得x=2、y=21或x=20、y=3
∴这个方程组的正整数解是(2,21,1)、(20,3,1),故此选项正确;
③关于x,y的方程组 ![]() ,其中﹣3≤a≤1,解得x=1+2a,y=1﹣a,x+y=2+a,
,其中﹣3≤a≤1,解得x=1+2a,y=1﹣a,x+y=2+a,
当a=1时,x+y=3,故方程组的解也是方程x+y=4﹣a=3的解,此选项正确.
故选:A.
【考点精析】通过灵活运用二元一次方程组的解和分式方程的解,掌握二元一次方程组中各个方程的公共解,叫做这个二元一次方程的解;分式方程无解(转化成整式方程来解,产生了增根;转化的整式方程无解);解的正负情况:先化为整式方程,求整式方程的解即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图,已知BA=AE=DC,AD=EC,CE⊥AE,垂足为E. 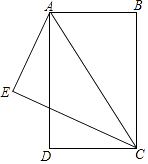
(1)求证:△DCA≌△EAC;
(2)只需添加一个条件,即 , 可使四边形ABCD为矩形.请加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+ax+b交x轴于A(1,0),B(3,0)两点,点P是抛物线上在第一象限内的一点,直线BP与y轴相交于点C. 
(1)求抛物线y=﹣x2+ax+b的解析式;
(2)当点P是线段BC的中点时,求点P的坐标;
(3)在(2)的条件下,求sin∠OCB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中xOy中,抛物线y=ax2﹣2ax﹣3a(a<0)与x轴交于A,B两点(点A在点B的左侧),经过点A的直线l:y=kx+b与y轴负半轴交于点C,与抛物线的另一个交点为D,且CD=4AC.
(1)求A、B两点的坐标及抛物线的对称轴;
(2)求直线l的函数表达式(其中k、b用含a的式子表示);
(3)点E是直线l上方的抛物线上的动点,若△ACE的面积的最大值为 ![]() ,求a的值;
,求a的值;
(4)设P是抛物线对称轴上的一点,点Q在抛物线上,以点A、D、P、Q为顶点的四边形能否成为矩形?若能,求出点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下说法: ①关于x的方程x+ ![]() =c+
=c+ ![]() 的解是x=c(c≠0);
的解是x=c(c≠0);
②方程组 ![]() 的正整数解有2组;
的正整数解有2组;
③已知关于x,y的方程组 ![]() ,其中﹣3≤a≤1,当a=1时,方程组的解也是方程x+y=4﹣a的解;
,其中﹣3≤a≤1,当a=1时,方程组的解也是方程x+y=4﹣a的解;
其中正确的有( )
A.②③
B.①②
C.①③
D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将平行四边形ABCD的边AB延长至点E,使BE=AB,连接DE,EC,DE,交BC于点O. 
(1)求证:△ABD≌△BEC;
(2)连接BD,若∠BOD=2∠A,求证:四边形BECD是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠DAC=∠ACB,要使四边形ABCD成为平行四边形,则应增加的条件不能是( ) 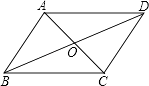
A.AD=BC
B.OA=OC
C.AB=CD
D.∠ABC+∠BCD=180°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com