
【题目】某烤鸭店在确定烤鸭的烤制时间时,主要依据的是如表数据:
鸭的质量/千克 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 |
烤制时间/分钟 | 40 | 60 | 80 | 100 | 120 | 140 | 160 |
设鸭的质量为x千克,烤制时间为t,估计当x=2.2千克时,t的值为_____.
【答案】108.
【解析】
观察表格可知,烤鸭的质量每增加0.5千克,烤制时间增加20分钟,由此可判断烤制时间是烤鸭质量的--次函数,设烤制时间为t分钟,烤鸭的质量为x千克,t与x的一次函数关系式为:t=kx+b,取(1,60),(2,100)代入,运用待定系数法求出函数关系式,再将x=2.2千克代入即可求出烤制时间.
从表中可以看出,烤鸭的质量每增加0.5千克,烤制的时间增加20分钟,由此可知烤制时间是烤鸭质量的一次函数.
设烤制时间为t分钟,烤鸭的质量为x千克,t与x的一次函数关系式为:t=kx+b,
![]() ,
,
解得![]() ,
,
所以t=40x+20.
当x=2.2千克时,t=40×2.2+20=108.
故答案为:108.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC

①求证:△ABE≌△CBD;
②若∠CAE=30°,求∠BDC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,M是AB上的动点
,M是AB上的动点![]() 不与A、B重合
不与A、B重合![]() ,过点M作
,过点M作![]() 交AC于点N,以MN为直径作
交AC于点N,以MN为直径作![]() ,并在
,并在![]() 内作内接矩形
内作内接矩形![]() 设
设![]() .
.
![]() 的面积
的面积![]() ______,
______,![]() ______;
______;![]() 用含x的代数式表示
用含x的代数式表示![]()
![]() 在动点M的运动过程中,设
在动点M的运动过程中,设![]() 与四边形MNCB重合部分的面积为
与四边形MNCB重合部分的面积为![]() 试求y关于x的函数表达式,并求出x为何值时,y的值最大,最大值为多少?
试求y关于x的函数表达式,并求出x为何值时,y的值最大,最大值为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
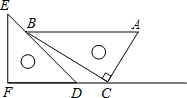
【题目】三角板是我们学习数学的好帮手.将一对直角三角板如图放置,点C在FD的延长线上,点B在ED上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,则CD的长度是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD⊥AB于点D,点E在CD上,下列四个条件:①AD=ED;②∠A=∠BED;③∠C=∠B;④AC=EB,将其中两个作为条件,不能判定△ADC≌△EDB的是

A.①②B.①④C.②③D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,△ABC为等边三角形,点D为AC上的一个动点,点E为BC延长线上一点,且BD=DE.
(1)如图1,若点D在边AC上,猜想线段AD与CE之间的关系,并说明理由;

图1
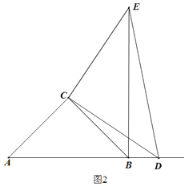
(2)如图2,若点D在AC的延长线上,(1)中的结论是否成立,请说明理由.

图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校.以下是他本次上学所用的时间与路程的关系示意图.
根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是多少米?
(2)在整个上学的途中哪个时间段小明骑车速度最快,最快的速度是多少米/分?
(3)小明在书店停留了多少分钟?
(4)本次上学途中,小明一共行驶了多少米?一共用了多少分钟?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合探究
问题情境:
我们在第十一章《三角形》中学习了三角形的边与角的性质,在第十二章《全等三角形》中学习了全等三角形的性质和判定.在一些探究题中经常用以上知识转化角和边,进而解决问题.
问题初探:
如图1,在△ABC中,∠ACB=90°,AC=BC,点D为直线AB上的一个动点(D与A,B不重合),连接CD,以CD为直角边作等腰直角三角形CDE,连接BE.


(1)当点D在线段AB上时,AD与BE的数量关系是 ;位置关系是 ;AB,BD,BE三条线段之间的关系是 .
类比再探:
(2)如图2,当点D运动到AB的延长线上时,AD与BE还存在(1)中的位置关系吗?若存在,请说明理由.同时探索AB,BD,BE三条线段之间的数量关系,并说明理由.
能力提升:
(3)如图3,当点D运动到BA的延长线上时,若AB=7,AD=2,则AE= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com