
| 1 |
| a |
| 1 |
| b |
| a2-b2 |
| ab |
|
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 在“五•一”劳动节期间,某商场为吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成20份),并规定:顾客每购物满200元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准标有数字的区域(未标数字的视为0),则顾客就可以分别获得该区域相应数字的返金券,凭返金券可以在该商场继续购物.若顾客不愿意转转盘,则每购物满200元可享受九五折优惠.
在“五•一”劳动节期间,某商场为吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成20份),并规定:顾客每购物满200元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准标有数字的区域(未标数字的视为0),则顾客就可以分别获得该区域相应数字的返金券,凭返金券可以在该商场继续购物.若顾客不愿意转转盘,则每购物满200元可享受九五折优惠.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 3 |
| 3 |
| 3 |
| 11 |
| 21 |
| 123 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,平行四边形ABCD中,AB=3,BC=5,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F.
如图,平行四边形ABCD中,AB=3,BC=5,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:
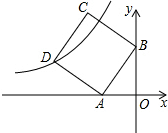 如图,在平面直角坐标系中,直线y=2x+4与x轴、y轴分别交于A、B两点,以AB为边在第二象限作正方形ABCD,点D在双曲线y=
如图,在平面直角坐标系中,直线y=2x+4与x轴、y轴分别交于A、B两点,以AB为边在第二象限作正方形ABCD,点D在双曲线y=| k |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com