
| A. | 4 | B. | $\sqrt{10}$ | C. | 2$\sqrt{2}$ | D. | 10 |
分析 根据平均数的计算公式先算出这组数据的平均数,再根据方差公式进行计算即可.
解答 解:这组数据的平均数为$\frac{1}{5}$×(1+2+3+4+10)=4,
则方差为$\frac{1}{5}$×[(1-4)2+(2-4)2+(3-4)2+(4-4)2+(10-4)2]=10,
故选:D.
点评 本题考查了方差和平均数:一般地设n个数据,x1,x2,…xn的平均数为$\overline{x}$,则方差S2═$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2].它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
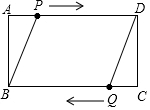 如图,在矩形ABCD中,AB=4cm,AD=6cm,点P从点A出发,以1cm/s的速度沿AD向终点D运动,同时,点Q从点C出发,以1cm/s的速度沿CB向终点B运动,设运动时间为t(s).
如图,在矩形ABCD中,AB=4cm,AD=6cm,点P从点A出发,以1cm/s的速度沿AD向终点D运动,同时,点Q从点C出发,以1cm/s的速度沿CB向终点B运动,设运动时间为t(s).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 商场 | 优惠活动 |
| 甲 | 全场按标价的6折销售 |
| 乙 | 实行“满100元送100元的购物券”的优惠,购物券可以在再购买时冲抵现金 (比如:顾客购衣服220元,赠券200元,再购买裤子时可冲抵现金,不再送券) |
| 丙 | 实行“满100元减50元的优惠”(比如:某顾客购物220元,他只需付款120元) |
| 商场 | 甲商场 | 乙商场 | 丙商场 |
| 实际付款(元) | 336 | 360 | 310 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
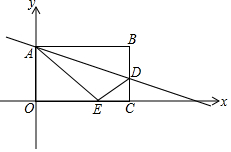 以矩形OABC的OC边所在直线为x轴,OA边所在直线为y轴建立平面直角坐标系如图所示,已知OA=8,OC=10,将矩形OABC沿直线AD折叠,点B恰好落在x轴上的点E处.
以矩形OABC的OC边所在直线为x轴,OA边所在直线为y轴建立平面直角坐标系如图所示,已知OA=8,OC=10,将矩形OABC沿直线AD折叠,点B恰好落在x轴上的点E处.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
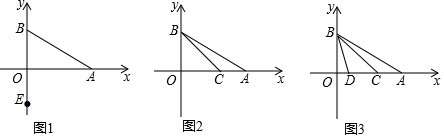
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
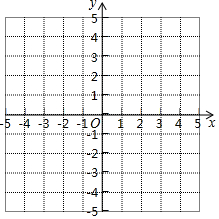 已知△ABC的三个顶点的坐标分别是A(-2,3),点B(0,1),点C(2,2).
已知△ABC的三个顶点的坐标分别是A(-2,3),点B(0,1),点C(2,2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com