
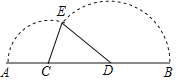
ЁОЬтФПЁПШчЭМЃЌвбжЊЯпЖЮABЃН12cmЃЌCЪЧЯпЖЮABЩЯвЛЖЈЕуЃЌЧвACЃН3cmЃЌЕуDЪЧЯпЖЮBCЩЯЕФвЛИіЖЏЕуЃЌЩшCDЃНxcmЃЌвдCЮЊжааФЫГЪБеыа§зЊЯпЖЮACвдDЮЊжааФЃЌФцЪБеыа§зЊЯпЖЮDBЃЌЪЙAЁЂBСНЕуФмжиКЯгкЕуEЃЎ
ЃЈ1ЃЉЕБCЁЂDЁЂEШ§ЕуФмЙЙГЩШ§НЧаЮЪБЃЌЧѓxЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉЕБxЮЊКЮжЕЪБЃЌЁїCDEЪЧжБНЧШ§НЧаЮЃП
ЃЈ3ЃЉМЧЁїCDEЕФУцЛ§ЮЊScm2ЃЌЪдЧѓГіSгыxЕФКЏЪ§БэДяЪНЃЛШєЁїCDEЕФУцЛ§ЮЊ![]() cm2ЃЌЪдШЗЖЈДЫЪБЕуDЕФЮЛжУЃП
cm2ЃЌЪдШЗЖЈДЫЪБЕуDЕФЮЛжУЃП
ЁОД№АИЁПЃЈ1ЃЉ3ЃМxЃМ6ЃЛЃЈ2ЃЉЕБxЃН4Лђ5ЪБЃЌЁїCDEЪЧжБНЧШ§НЧаЮЃЛЃЈ3ЃЉSЃН![]() ЃЛЕБSЃН
ЃЛЕБSЃН![]() ЪБЃЌDгыЕуCЕФОрРыЮЊ
ЪБЃЌDгыЕуCЕФОрРыЮЊ![]() cmЛђ
cmЛђ![]() cmЃЎ
cmЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩACЃНCEЃН3ЃЌABЃН12ЃЌCDЃНxжЊDEЃНBDЃН9ЉxЃЌРћгУШ§НЧаЮШ§БпЙиЯЕПЩЕУД№АИЃЛ
ЃЈ2ЃЉЗжЁЯDCEЃН90ЁуЃЌЁЯCDEЃН90ЁуКЭЁЯCEDЃН90ЁуШ§жжЧщПіЃЌРћгУЙДЙЩЖЈРэСаГіЗНГЬЃЌНтжЎПЩЕУЃЛ
ЃЈ3ЃЉзїEFЁЭABЃЌЩшCFЃНmЃЌЁїCDEЕФУцЛ§ЮЊSЃЌИљОнEF2ЃН9Љm2ЃНЃЈ9ЉxЃЉ2ЉЃЈxЉmЃЉ2ЕУmЃН![]() ЃЌгЩSЃН
ЃЌгЩSЃН![]() CDEFжЊS2ЃН
CDEFжЊS2ЃН![]() CD2EF2НЋЯрЙиЪ§ОнДњШыЃЌећРэПЩЕУКЏЪ§НтЮіЪНЃЌдйИљОнЬтвтСаГіЗНГЬНтжЎПЩЕУЃЎ
CD2EF2НЋЯрЙиЪ§ОнДњШыЃЌећРэПЩЕУКЏЪ§НтЮіЪНЃЌдйИљОнЬтвтСаГіЗНГЬНтжЎПЩЕУЃЎ
НтЃКЃЈ1ЃЉЁпACЃНCEЃН3ЃЌABЃН12ЃЌCDЃНxЃЌ
ЁрDEЃНBDЃН9ЉxЃЌ
гЩCD+CEЃОDEЧвCDЉCEЃМDE
ПЩЕУ![]() ЃЌ
ЃЌ
НтЕУЃК3ЃМxЃМ6ЃЛ
ЃЈ2ЃЉЂйЕБЁЯDCEЃН90ЁуЪБЃЌ
ИљОнЙДЙЩЖЈРэCD2+CE2ЃНDE2ЃЌМДx2+32ЃНЃЈ9ЉxЃЉ2ЃЌ
НтЕУЃКxЃН4ЃЛ
ЂкЕБЁЯCDEЃН90ЁуЪБЃЌ
ИљОнЙДЙЩЖЈРэCD2+DE2ЃНCE2ЃЌМДx2+ЃЈ9ЉxЃЉ2ЃН32ЃЌ
ећРэЃЌЕУЃКx2Љ9x+36ЃН0ЃЌ
гЩЁїЃНЃЈЉ9ЃЉ2Љ4ЁС1ЁС36ЃНЉ63ЃМ0жЊЗНГЬЮоНтЃЛ
ЂлЕБЁЯCEDЃН90ЁуЪБЃЌ
ИљОнЙДЙЩЖЈРэCE2+DE2ЃНCD2ЃЌМД32+ЃЈ9ЉxЃЉ2ЃНx2ЃЌ
НтЕУЃКxЃН5ЃЛ
злЩЯЃЌЕБxЃН4Лђ5ЪБЃЌЁїCDEЪЧжБНЧШ§НЧаЮЃЛ
ЃЈ3ЃЉЙ§ЕуEзїEFЁЭABгкЕуFЃЌ
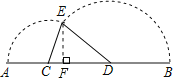
ЩшCFЃНmЃЌЁїCDEЕФУцЛ§ЮЊSЃЌ
дђЃКEF2ЃН9Љm2ЃНЃЈ9ЉxЃЉ2ЉЃЈxЉmЃЉ2ЃЌ
ЁрmЃН![]() ЃЌ
ЃЌ
ЁпSЃН![]() CDEFЃЌ
CDEFЃЌ
S2ЃН![]() CD2EF2
CD2EF2
ЃН![]() x2[9Љ
x2[9Љ![]() ]
]
ЃНЉ18ЃЈx2Љ9x+18ЃЉЃЌ
ЁрSЃН![]() ЃЌ
ЃЌ
ЕБSЃН![]() ЃН
ЃН![]() ЪБЃЌ
ЪБЃЌ
НтЕУЃКx1ЃН![]() ЃЌx2ЃН
ЃЌx2ЃН![]() ЃЌ
ЃЌ
ДЫЪБЕуDгыЕуCЕФОрРыЮЊ![]() cmЛђ
cmЛђ![]() cmЃЎ
cmЃЎ


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
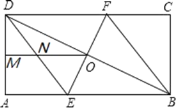
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌЙ§BDЕФжаЕуOзіEFЁЭBDЃЌЗжБ№гыABЁЂCDНЛгкЕуEЁЂF.СЌНгDEЁЂBF.
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮBEDFЪЧСтаЮЃЛ
ЃЈ2ЃЉШєMЪЧADжаЕуЃЌСЊНсOMгыDEНЛгкЕуNЃЌAD=OM=4ЃЌдђONЕФГЄЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
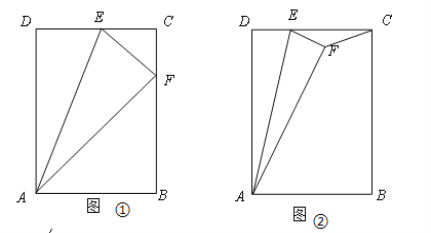
ЁОЬтФПЁПдкОиаЮABCDжаЃЌABЃН3ЃЌADЃН5ЃЌEЪЧЩфЯпDCЩЯЕФЕуЃЌСЌНгAEЃЌНЋЁїADEбижБЯпAEЗелЕУЁїAFEЃЎ
ЃЈ1ЃЉШчЭМЂйЃЌЕуFЧЁКУдкBCЩЯЃЌЧѓжЄЃКЁїABFЁзЁїFCEЃЛ
ЃЈ2ЃЉШчЭМЂкЃЌЕуFдкОиаЮABCDФкЃЌСЌНгCFЃЌШєDEЃН1ЃЌЧѓЁїEFCЕФУцЛ§ЃЛ
ЃЈ3ЃЉШєвдЕуEЁЂFЁЂCЮЊЖЅЕуЕФШ§НЧаЮЪЧжБНЧШ§НЧаЮЃЌдђDEЕФГЄЮЊ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЪЧЖўДЮКЏЪ§yЃНax2+bx+cЃЈaЃЌbЃЌcЪЧГЃЪ§ЃЌaЁй0ЃЉЭМЯѓЕФвЛВПЗжЃЌгыxжсЕФНЛЕуAдкЕуЃЈ2ЃЌ0ЃЉКЭЃЈ3ЃЌ0ЃЉжЎМфЃЌЖдГЦжсЪЧжБЯпxЃН1ЖдгкЯТСаЫЕЗЈЃКЂйabcЃМ0ЃЛЂк2a+bЃН0ЃЛЂл3a+cЃО0ЃЛ ЂмЕБЉ1ЃМxЃМ3ЪБЃЌyЃО0ЃЛЂнa+bЃОmЃЈam+bЃЉЃЈmЁй1ЃЉЃЌЦфжае§ШЗгаЃЈЁЁЁЁЃЉ
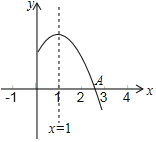
A.1ИіB.2ИіC.3ИіD.4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЕуAЃЌBЕФзјБъЗжБ№ЮЊЃЈ4ЃЌ0ЃЉЃЌЃЈ3ЃЌ2ЃЉЃЎ
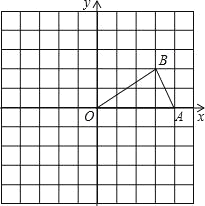
ЃЈ1ЃЉЛГіЁїAOBЙигкдЕуOЖдГЦЕФЭМаЮЁїCODЃЛ
ЃЈ2ЃЉНЋЁїAOBШЦЕуOАДФцЪБеыЗНЯђа§зЊ90ЁуЕУЕНЁїEOFЃЌЛГіЁїEOFЃЛ
ЃЈ3ЃЉЕуDЕФзјБъЪЧЁЁ ЁЁЃЌЕуFЕФзјБъЪЧЁЁ ЁЁЃЌДЫЭМжаЯпЖЮBFКЭDFЕФЙиЯЕЪЧЁЁ ЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЕШбќRtЁїABCжаЃЌЁЯABCЃН90ЁуЃЌABЃНBCЃЎЕуDЪЧЯпЖЮACЩЯвЛЕуЃЌСЌНгBDЃЎЙ§ЕуCзїCEЁЭBDгкЕуEЃЎЕуFЪЧABДЙжБЦНЗжЯпЩЯвЛЕуЃЌСЌНгBFЁЂEFЃЎ
ЃЈ1ЃЉШєADЃН4![]() ЃЌtanЁЯBCEЃН
ЃЌtanЁЯBCEЃН![]() ЃЌЧѓABЕФГЄЃЛ
ЃЌЧѓABЕФГЄЃЛ
ЃЈ2ЃЉЕБЕуFдкACБпЩЯЪБЃЌЧѓжЄЃКЁЯFECЃН45ЁуЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ![]() жаЃЌ
жаЃЌ![]() ЃЌPЪЧаББпACЩЯвЛИіЖЏЕуЃЌвдМДЮЊжБОЖзї
ЃЌPЪЧаББпACЩЯвЛИіЖЏЕуЃЌвдМДЮЊжБОЖзї![]() НЛBCгкЕуDЃЌгыACЕФСэвЛИіНЛЕуEЃЌСЌНгDEЃЎ
НЛBCгкЕуDЃЌгыACЕФСэвЛИіНЛЕуEЃЌСЌНгDEЃЎ
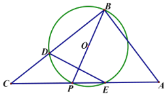
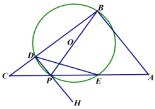
ЃЈ1ЃЉЕБ![]() ЪБЃЌ
ЪБЃЌ
ЂйШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЖШЪ§ЃЛ
ЕФЖШЪ§ЃЛ
ЂкЧѓжЄ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЕБ![]() ЃЌ
ЃЌ![]() ЪБЃЌ
ЪБЃЌ
ЂйЪЧКЌДцдкЕуPЃЌЪЙЕУ![]() ЪЧЕШбќШ§НЧаЮЃЌШєДцдкЧѓГіЫљгаЗћКЯЬѕМўЕФCPЕФГЄЃЛ
ЪЧЕШбќШ§НЧаЮЃЌШєДцдкЧѓГіЫљгаЗћКЯЬѕМўЕФCPЕФГЄЃЛ
ЂквдDЮЊЖЫЕуЙ§PзїЩфЯпDHЃЌзїЕуOЙигкDEЕФЖдГЦЕуQЧЁКУТфдк![]() ФкЃЌдђCPЕФШЁжЕЗЖЮЇЮЊ________ЃЎЃЈжБНгаДГіНсЙћЃЉ
ФкЃЌдђCPЕФШЁжЕЗЖЮЇЮЊ________ЃЎЃЈжБНгаДГіНсЙћЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкжБНЧзјБъЯЕxOyжаЃЌжБЯп![]() гыЫЋЧњЯп
гыЫЋЧњЯп![]() ЯрНЛгкAЃЈЃ1ЃЌaЃЉЁЂBСНЕуЃЌBCЁЭxжсЃЌДЙзуЮЊCЃЌЁїAOCЕФУцЛ§ЪЧ1ЃЎ
ЯрНЛгкAЃЈЃ1ЃЌaЃЉЁЂBСНЕуЃЌBCЁЭxжсЃЌДЙзуЮЊCЃЌЁїAOCЕФУцЛ§ЪЧ1ЃЎ
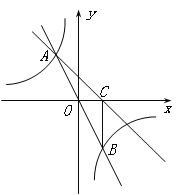
ЃЈ1ЃЉЧѓmЁЂnЕФжЕЃЛ
ЃЈ2ЃЉЧѓжБЯпACЕФНтЮіЪНЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
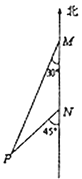
ЁОЬтФПЁП2019Фъ12дТ17ШеЃЌЮвЙњЕквЛЫвЙњВњКНФИЁАЩНЖЋНЂЁБдкКЃФЯШ§бЧНЛИЖКЃОќ.ШчЭМЃЌЁАЩНЖЋНЂЁБдквЛДЮЪдЫЎВтЪджаЃЌКНаажС![]() ДІЃЌЙлВтжИЛгЫў
ДІЃЌЙлВтжИЛгЫў![]() ЮЛгкФЯЦЋЮї
ЮЛгкФЯЦЋЮї![]() ЗНЯђЃЌдкбие§ФЯЗНЯђвд30КЃРя/аЁЪБЕФЫйЖШдШЫйКНаа2аЁЪБКѓЃЌЕНДя
ЗНЯђЃЌдкбие§ФЯЗНЯђвд30КЃРя/аЁЪБЕФЫйЖШдШЫйКНаа2аЁЪБКѓЃЌЕНДя![]() ДІЃЌдйЙлВтжИЛгЫў
ДІЃЌдйЙлВтжИЛгЫў![]() ЮЛгкФЯЦЋЮї
ЮЛгкФЯЦЋЮї![]() ЗНЯђЃЌШєМЬајЯђФЯКНаа.ЧѓЁАЩНЖЋНЂЁБгыжИЛгЫўжЎМфЕФзюНќОрРыЮЊЖрЩйКЃРяЃПЃЈНсЙћБЃСєИљКХЃЉ
ЗНЯђЃЌШєМЬајЯђФЯКНаа.ЧѓЁАЩНЖЋНЂЁБгыжИЛгЫўжЎМфЕФзюНќОрРыЮЊЖрЩйКЃРяЃПЃЈНсЙћБЃСєИљКХЃЉ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com