
【题目】如图,在等腰Rt△ABC中,∠ABC=90°,AB=BC.点D是线段AC上一点,连接BD.过点C作CE⊥BD于点E.点F是AB垂直平分线上一点,连接BF、EF.
(1)若AD=4![]() ,tan∠BCE=
,tan∠BCE=![]() ,求AB的长;
,求AB的长;
(2)当点F在AC边上时,求证:∠FEC=45°.

【答案】(1) AB=18;(2)证明见解析;
【解析】
(1)先过点D作DM⊥AB于点M,构造等腰直角三角形,求得DM=AM=4,再根据∠ABD=∠BCE,得出tan∠BCE=tan∠ABD,求得BM=14,进而根据AB=AM+BM进行计算;
(2)在CE上截取CN=BE,连接FN,先判定△BEF≌△CFN,得出△EFN是等腰直角三角形,根据等腰三角形的性质即可得到结论.
(1)如图,过点D作DM⊥AB于点M.
∵∠ABC=90°,AB=BC,∴∠A=45°,∴AM=DM.
∵AD=4![]() ,∴DM=AM
,∴DM=AM![]() AD=4.
AD=4.
∵CE⊥BD,∴∠BEC=90°=∠ABC,∴∠BCE+∠EBC=90,∠EBC+∠ABD=90°,∴∠ABD=∠BCE,∴tan∠BCE=tan∠ABD![]() ,即
,即![]() ,∴BM=14,∴AB=AM+BM=4+14=18;
,∴BM=14,∴AB=AM+BM=4+14=18;
(2)∵F是AB的垂直平分线上的点,∴AF=BF,∴∠A=∠ABF=45°.
∵∠ABC=90°,∴∠FBC=45°,∴∠FBC=∠FCB,且∠ABD=∠BCE,∴BF=CF,∠EBF=∠ECF,如图,在CE上截取CN=BE,连接FN.
∵BF═CF,∠EBF=∠ECF,∴△BEF≌△CFN,(SAS),∴FN=EF,∠BFE=∠CFN.
∵∠FCB=∠FBC=45°,∴∠BFC=90°,∴∠CFN+∠BFN=90°,∴∠BFE+∠BFN=90°,∴∠EFN=90°,且EF=FN,∴△EFN是等腰直角三角形,∴∠FEC=45°.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,半径OC=6,D为半径OC上异于O,C的点,过点D作AB⊥OC,交⊙O于A,B,点E在线段AB上,AE=CE,点P在线段EC的延长线上,PB=PE.
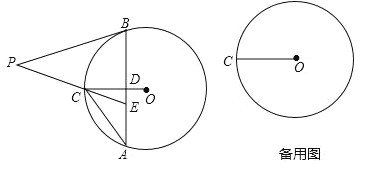
(1)若OD=2,求弦AB的长;
(2)当点D在线段OC(不含端点)上移动时,直线PB与⊙O有怎样的位置关系?请说明理由;
(3)点Q是⊙O上的一个动点,若点D为OC中点时,线段PQ的最小值为多少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
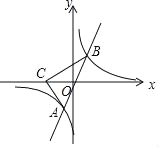
【题目】如图,直线y=3x与双曲线y=![]() 相交于点A,B,点C的坐标是(-4,0),且AO=AC.
相交于点A,B,点C的坐标是(-4,0),且AO=AC.
(1)求双曲线的解析式.
(2)已知A、B两点关于原点对称,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
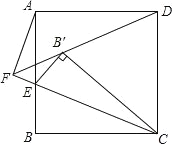
【题目】如图,E为正方形ABCD边AB上的一点,且AB=3,BE=1.将△CBE翻折得到△CB'E,连接并延长DB'与CE延长线相交于点F,连接AF,则AF的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=kx(k≠0)经过点(12,﹣5),将直线向上平移m(m>0)个单位,若平移后得到的直线与半径为6的⊙O相交(点O为坐标原点),则m的取值范围为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超速行驶是引发交通事故的主要原因之一,小明和三位同学尝试用自己所学的知识检测车速,如图,观测点设在A处,距离大路(BC)为30米,一辆小轿车由西向东匀速行驶,测得此车从B处到C处所用的时间为5秒,∠BAC=60°.
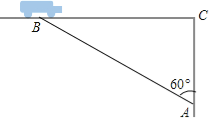
(1)求B、C两点间的距离.
(2)请判断此车是否超过了BC路段限速40千米/小时的速度.(参考数据:![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,BC=8 AB=6cm,动点P从点A开始沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是( )
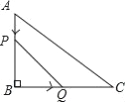
A. 18cm2 B. 12cm2 C. 9cm2 D. 3cm2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com