
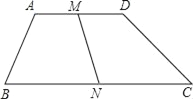
【题目】在梯形ABCD中,AD∥BC,∠B+∠C=90°,AB=5,CD=12,M,N分别为AD,BC的中点,则线段MN=_____.
【答案】6.5
【解析】
过点M作ME∥AB,MF∥CD,由此得到∠MEN=∠B,∠NFM=∠C,又∠B+∠C=90°,可以推出∠EMF=90°,然后根据平行四边形的性质可以得到ME=AB=5,MF=CD=12,AM=DM,BN=CN,再利用斜边上的中线等于斜边的一半即可证明MN=![]() EF,最后就可以求出MN.
EF,最后就可以求出MN.
解:如图:
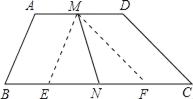
过点M作ME∥AB,MF∥CD,
∴∠MEN=∠B,∠NFM=∠C,
∵∠B+∠C=90°,
∴∠MEF+∠MFE=90°,
∴∠EMF=90°.
∵AD∥BC,
∴ME=AB=5,MF=CD=12,AM=DM,BN=CN.
∴EF=13,EN=FN.
∴MN=![]() EF=6.5.
EF=6.5.
故答案为:6.5


科目:初中数学 来源: 题型:
【题目】(本题10分)如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线,交AB于点E,交CA的延长线于点F.
(1)求证:FE⊥AB;
(2)当EF=6,![]() =
=![]() 时,求DE的长.
时,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
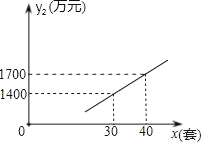
【题目】国家推行“节能减排,低碳经济”政策后,某环保节能设备生产企业的产品供不应求,若该企业的某种环保设备每月的产量保持在一定的范国,每套产品的售价不低于90万元,生产总成本不高于1250万元,已知这种设备的月产量x(套)与每套产品的售价y1(万元)之间满足关系式y1=130﹣x,月产量x(套)与生产总成本y2(万元)存在如图所示的函数关系.
(1)求出y2与x之间的函数关系式,并求月产量x的范围;
(2)当月产量x(套)为多少时,这种设备的利润W(万元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠ABC=90°,AB=BC.点D是线段AC上一点,连接BD.过点C作CE⊥BD于点E.点F是AB垂直平分线上一点,连接BF、EF.
(1)若AD=4![]() ,tan∠BCE=
,tan∠BCE=![]() ,求AB的长;
,求AB的长;
(2)当点F在AC边上时,求证:∠FEC=45°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AC平分∠DAB,AC2=ABAD,∠ADC=90°,点E为AB的中点.
(1)求证:△ADC∽△ACB.
(2)若AD=2,AB=3,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E、F分别是 四边形ABCD的边AB、CD上的点,AF与DE相交于点P,BF与CE相交于点Q,记S1=S△APD,S2=S△BQC,四边形EQFP的面积为S.
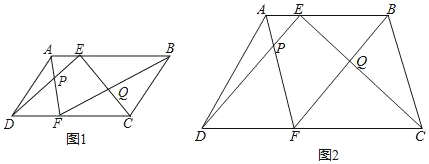
(1)若四边形ABCD为平行四边形,如图1,求证:S=S1+S2;
(2)若四边形ABCD为一般凸多边形,AB∥CD,如图2,求证:S=S1+S2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从热气球C处测得地面A、B两点的俯角分别为45°、30°,如果此时热气球C处离地面的高度CD为100米,且点A、D、B在同一直线上,求AB两点间的距离(结果保留根号)
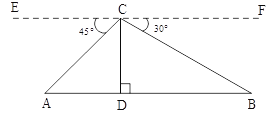
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处距离灯塔P有多远?(结果用非特殊角的三角函数表示即可)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在开展“学雷锋社会实践”活动中,某校为了解全校1200名学生参加活动的情况,随机调查了50名学生每人参加活动的次数,并根据数据绘成条形统计图如下:
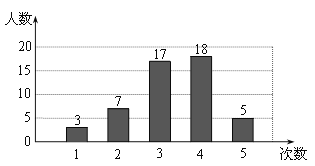
(Ⅰ)求这50个样本数据的平均数、众数和中位数;
(Ⅱ)根据样本数据,估算该校1200名学生共参加了多少次活动.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com