
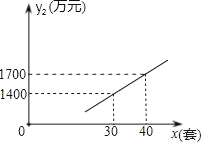
����Ŀ���������������ܼ��ţ���̼���������ߺ�ij���������豸������ҵ�IJ�Ʒ����Ӧ��������ҵ��ij�ֻ����豸ÿ�µIJ���������һ���ķ�����ÿ�ײ�Ʒ���ۼ۲�����90��Ԫ�������ܳɱ�������1250��Ԫ����֪�����豸���²���x���ף���ÿ�ײ�Ʒ���ۼ�y1����Ԫ��֮�������ϵʽy1��130��x���²���x���ף��������ܳɱ�y2����Ԫ��������ͼ��ʾ�ĺ�����ϵ��
��1�����y2��x֮��ĺ�����ϵʽ�������²���x�ķ�Χ��
��2�����²���x���ף�Ϊ����ʱ�������豸������W����Ԫ�������������Ƕ��٣�
���𰸡���1��������ϵʽy2��30x+500��x��25����2�����²���Ϊ35��ʱ������������������1950��Ԫ��
��������
��1���躯����ϵʽΪy2=kx+b���ѣ�30��1400����40��1700��������⼴�ɣ���������������ÿ�ײ�Ʒ�������ۼ۲�����90��Ԫ�������ܳɱ�������1250��Ԫ���г�����ʽ������²���x�ķ�Χ��
��2�����ݵ�����ϵ���豸������=ÿ̨���ۼ����²���-�����ܳɱ����г�������ϵʽ������ֵ��
��1���躯����ϵʽΪy2=kx+b�������꣨30��1400����40��1700�����룬
![]() ����ã�
����ã�![]() ��
��
�ຯ����ϵʽy2=30x+500��
������ã�![]() ��
��
��ã�x��25��
���²���x�ķ�ΧΪ��x��25��
��2����W=xy1-y2=x��170-2x��-��500+30x��=-2x2+140x-500
��W=-2��x-35��2+1950
��25��35��40��
�൱x=35ʱ��W���=1950
�𣺵��²���Ϊ35��ʱ������������������1950��Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
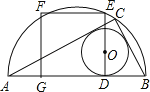
����Ŀ����ͼ��ABΪ��Բ��ֱ����C�ǰ�Բ����һ�㣬������DEFG��һ��DG��ֱ��AB�ϣ���һ��DE����ABC������ԲԲ��O���ҵ�E�ڰ�Բ���ϣ���������DEFG�����Ϊ100���ҡ�ABC������Բ�뾶r=4�����Բ��ֱ��AB=____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һԪ���η�����ʵ������Ϊ��4���ǣ� ��
A. x2+2x��4=0 B. x2��4x+4=0 C. x2+4x+10=0 D. x2+4x��5=0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
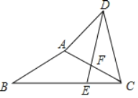
����Ŀ����֪���ڡ�ABC�У�AB��AC��6����B��30�㣬EΪBC��һ�㣬BE��2EC��DE��DC����ADC��60�㣬��AD�ij�_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
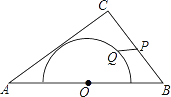
����Ŀ����ͼ������ABC�У�AB=5��AC=4��BC=3���Ա�AB���е�OΪԲ�ģ�����Բ��AC���У���P��Q�ֱ��DZ�BC�Ͱ�Բ�ϵĶ��㣬����PQ����PQ�������ֵ����Сֵ�ĺ���________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y��3x��˫����y��![]() �ཻ�ڵ�A��B����C����������-4��0������AO��AC��
�ཻ�ڵ�A��B����C����������-4��0������AO��AC��
(1)��˫���ߵĽ���ʽ��
(2)��֪A��B�������ԭ��Գƣ����ABC�������
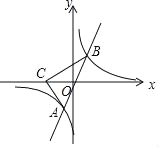
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��EΪ������ABCD��AB�ϵ�һ�㣬��AB��3��BE��1������CBE���۵õ���CB'E�����Ӳ��ӳ�DB'��CE�ӳ����ཻ�ڵ�F������AF����AF�ij�Ϊ_____��
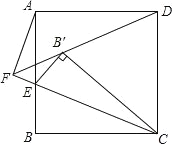
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ABCD�У�AD��BC����B+��C��90�㣬AB��5��CD��12��M��N�ֱ�ΪAD��BC���е㣬���߶�MN��_____��
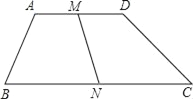
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�����������¡����̡����ࡢ�������ij�������ӭ��2011����˻���ٿ���������ȫ��ʵʩ������ò���������ж���ij���̶ӳе���һ�γ�Ϊ1500�ĵ�·�̻����̣�ʩ��ʱ�������̻��������������̻�1�ĵ�·��ҪA�ͻ�2֦��B�ͻ�3֦���ɱ���22Ԫ���ҷ������̻�1�ĵ�·��ҪA�ͻ�1֦��B�ͻ�5֦���ɱ���25Ԫ����Ҫ�����ҷ����̻���·���ܳ��Ȳ������ڰ������̻���·���ܳ��ȵ�2��.
��1����A�ͻ���B�ͻ�ÿ֦�ijɱ��ֱ��Ƕ���Ԫ��
��2���������̻��ĵ�·�ܳ���Ϊ������ʱ�����蹤�̵��ܳɱ����٣��ܳɱ������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com