
【题目】如图,AB为半圆的直径,C是半圆弧上一点,正方形DEFG的一边DG在直径AB上,另一边DE过△ABC的内切圆圆心O,且点E在半圆弧上.若正方形DEFG的面积为100,且△ABC的内切圆半径r=4,则半圆的直径AB=____.
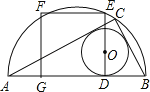
【答案】21
【解析】
连接EB、AE,OJ、OI,可得OHCI是正方形,且边长是4,可设BD=x,AD=y,则BD=BH=x,AD=AI=y,分别利用直角三角形ABC和直角三角形AEB中的勾股定理和相似比作为相等关系列方程组求解即可求得半圆的直径AB=21.
∵正方形DEFG的面积为100,
∴正方形DEFG边长为10.
连接EB、AE,OI、OJ,
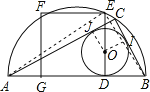
∵AC、BC是⊙O的切线,
∴CJ=CI,∠OJC=∠OIC=90°,
∵∠ACB=90°,
∴四边形OICJ是正方形,且边长是4,
设BD=x,AD=y,则BD=BI=x,AD=AJ=y,
在Rt△ABC中,由勾股定理得(x+4)2+(y+4)2=(x+y)2①;
在Rt△AEB中,
∵∠AEB=90°,ED⊥AB,
∴△ADE∽△BDE∽△ABE,
∴ED2=ADBD,即102=xy②.
解①、②得x+y=21,即半圆的直径AB=21.
故答案为:21.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】韦达定理:若一元二次方程ax2+bx+c=0(a≠0)的两根分别为x1、x2 , 则x1+x2=﹣![]() , x1x2=
, x1x2=![]() , 阅读下面应用韦达定理的过程:
, 阅读下面应用韦达定理的过程:
若一元二次方程﹣2x2+4x+1=0的两根分别为x1、x2 , 求x12+x22的值.
解:该一元二次方程的△=b2﹣4ac=42﹣4×(﹣2)×1=24>0
由韦达定理可得,x1+x2=﹣![]() =﹣
=﹣![]() =2,x1x2=
=2,x1x2=![]() =
=![]() =﹣
=﹣![]()
x12+x22=(x1+x2)2﹣2x1x2
=22﹣2×(﹣![]() )
)
=5
然后解答下列问题:
(1)设一元二次方程2x2+3x﹣1=0的两根分别为x1,x2, 不解方程,求x12+x22的值;
(2)若关于x的一元二次方程(k﹣1)x2+(k2﹣1)x+(k﹣1)2=0的两根分别为α,β,且α2+β2=4,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.
(1)求证:△CDB≌△BAG.
(2)如果四边形BFDE是菱形,那么四边形AGBD是什么特殊四边形?并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
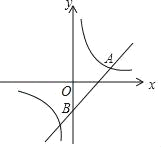
【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)与反比例函数y=![]() (m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(1)求反比例函数和一次函数的表达式;
(2)如果点P是x轴上的一点,且△ABP的面积是3,求点P的坐标;
(3)若P是坐标轴上一点,且满足PA=OA,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲班56人,其中身高在160厘米以上的男同学10人,身高在160厘米以上的女同学3人,乙班80人,其中身高在160厘米以上的男同学20人,身高在160厘米以上的女同学8人.如果想在两个班的160厘米以上的女生中抽出一个作为旗手,在哪个班成功的机会大?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分10分)如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() 为常数,且
为常数,且![]() )的图象交于A(1,a)、B两点.
)的图象交于A(1,a)、B两点.
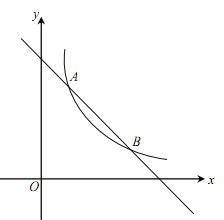
(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题10分)如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线,交AB于点E,交CA的延长线于点F.
(1)求证:FE⊥AB;
(2)当EF=6,![]() =
=![]() 时,求DE的长.
时,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
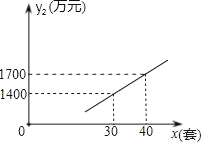
【题目】国家推行“节能减排,低碳经济”政策后,某环保节能设备生产企业的产品供不应求,若该企业的某种环保设备每月的产量保持在一定的范国,每套产品的售价不低于90万元,生产总成本不高于1250万元,已知这种设备的月产量x(套)与每套产品的售价y1(万元)之间满足关系式y1=130﹣x,月产量x(套)与生产总成本y2(万元)存在如图所示的函数关系.
(1)求出y2与x之间的函数关系式,并求月产量x的范围;
(2)当月产量x(套)为多少时,这种设备的利润W(万元)最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com