
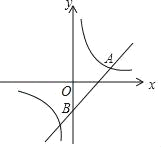
【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)与反比例函数y=![]() (m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(1)求反比例函数和一次函数的表达式;
(2)如果点P是x轴上的一点,且△ABP的面积是3,求点P的坐标;
(3)若P是坐标轴上一点,且满足PA=OA,直接写出点P的坐标.
【答案】(1)y=![]() ;y=x﹣2;(2)点P的坐标为(0,0)、(4,0);(3)点P的坐标为(6,0)或(0,2).
;y=x﹣2;(2)点P的坐标为(0,0)、(4,0);(3)点P的坐标为(6,0)或(0,2).
【解析】
(1)将点A(3,1)代入y=![]() ,利用待定系数法求得反比例函数的解析式,再将点A(3,1)和B(0,-2)代入y=kx+b,利用待定系数法求得一次函数的解析式;
,利用待定系数法求得反比例函数的解析式,再将点A(3,1)和B(0,-2)代入y=kx+b,利用待定系数法求得一次函数的解析式;
(2)首先求得AB与x轴的交点C的坐标,然后根据S△ABP=S△ACP+S△BCP即可列方程求得P的横坐标;
(3)分两种情况进行讨论:①点P在x轴上;②点P在y轴上.根据PA=OA,利用等腰三角形的对称性求解.
(1)∵反比例函数y=![]() (m≠0)的图象过点A(3,1),
(m≠0)的图象过点A(3,1),
∴3=![]() ,解得m=3.
,解得m=3.
∴反比例函数的表达式为y=![]() .
.
∵一次函数y=kx+b的图象过点A(3,1)和B(0,-2),
∴![]() ,
,
解得:![]() ,
,
∴一次函数的表达式为y=x-2;
(2)如图,设一次函数y=x-2的图象与x轴的交点为C.
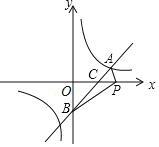
令y=0,则x-2=0,x=2,
∴点C的坐标为(2,0).
∵S△ABP=S△ACP+S△BCP=3,
∴![]() PC×1+
PC×1+![]() PC×2=3,
PC×2=3,
∴PC=2,
∴点P的坐标为(0,0)、(4,0);
(3)若P是坐标轴上一点,且满足PA=OA,则P点的位置可分两种情况:

①如果点P在x轴上,那么O与P关于直线x=3对称,
所以点P的坐标为(6,0);
②如果点P在y轴上,那么O与P关于直线y=1对称,
所以点P的坐标为(0,2).
综上可知,点P的坐标为(6,0)或(0,2).


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
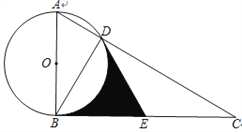
【题目】如图,Rt△ABC中,∠ABC为直角,以AB为直径作⊙O交AC于点D,点E为BC中点,连结DE,DB.
(1)求证:DE与⊙O相切;
(2)若∠C=30°,求∠BOD的度数;
(3)在(2)的条件下,若⊙O半径为2, 求阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果店张阿姨以每斤4元的价格购进某种水果若干斤,然后以每斤6元的价格出售,每天可售出150斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出30斤,为保证每天至少售出360斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利450元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知y=(m2+m)![]() +(m﹣3)x+m2是x的二次函数,求出它的解析式.
+(m﹣3)x+m2是x的二次函数,求出它的解析式.
(2)用配方法求二次函数y=﹣x2+5x﹣7的顶点坐标并求出函数的最大值或最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,⊿ABC中,AB=AC,以AB为直径的⊙O交BC于点P,PD⊥AC于点D.
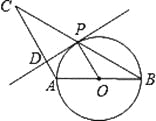
(1)求证:PD是⊙O的切线.
(2)若∠CAB=120°,AB=2,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )

A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
查看答案和解析>>
科目:初中数学 来源: 题型:
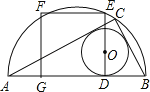
【题目】如图,AB为半圆的直径,C是半圆弧上一点,正方形DEFG的一边DG在直径AB上,另一边DE过△ABC的内切圆圆心O,且点E在半圆弧上.若正方形DEFG的面积为100,且△ABC的内切圆半径r=4,则半圆的直径AB=____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,半径OC=6,D为半径OC上异于O,C的点,过点D作AB⊥OC,交⊙O于A,B,点E在线段AB上,AE=CE,点P在线段EC的延长线上,PB=PE.
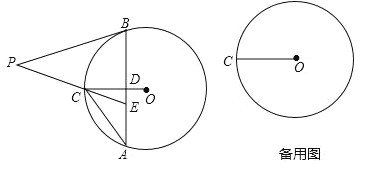
(1)若OD=2,求弦AB的长;
(2)当点D在线段OC(不含端点)上移动时,直线PB与⊙O有怎样的位置关系?请说明理由;
(3)点Q是⊙O上的一个动点,若点D为OC中点时,线段PQ的最小值为多少?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com