
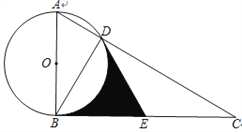
【题目】如图,Rt△ABC中,∠ABC为直角,以AB为直径作⊙O交AC于点D,点E为BC中点,连结DE,DB.
(1)求证:DE与⊙O相切;
(2)若∠C=30°,求∠BOD的度数;
(3)在(2)的条件下,若⊙O半径为2, 求阴影部分面积.
【答案】(1)证明见解析;
(2)∠BOD=120°;
(3)S阴影部分=![]()
【解析】试题分析:(1)、连接OD,根据直径得出∠BDC=90°,根据直角三角形斜边上的中线的性质得出∠BDE=∠DBE,根据OD=OB得出∠ODB=∠OBD,从而得出∠ODE为直角,得出切线;(2)、根据直角三角形的性质得出∠DEB=60°,根据四边形OBED的内角和得出∠BOD的度数;(3)、根据阴影部分的面积等于四边形OBED的面积减去扇形OBD的面积得出答案.
试题解析:(1)连结OD,∵AB为⊙O为直径 ∴∠ADB=90°则∠BDC=90°,
又∵E是斜边BC的中点 ∴DE=BE=CE, ∴∠BDE=∠DBE
∵OD=OB,∴∠ODB=∠OBD
∴∠ODE=∠ODB+∠BDE=∠OBD+∠DBE=∠ABC=90°
即DE与⊙O相切
(2)若∠C=30°而DE=CE ∴∠DEB=60°
在四边形OBED中, 则∠BOD=360°-90°-90°-60°=120°
(3)连结OE,则∠OED=∠OEB=30°
∵OD=OB=2 ∴DE=BE=2![]()
∴S阴影部分=S四边形OBED-S扇形OBD=S△OBE+S△ODE-S扇形OBD
=2![]() +2
+2![]() -
-![]() =4
=4![]() -
-![]()


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
【题目】a,b是有理数,它们在数轴上的对应点的位置如图所示:把a,﹣a,b,﹣b按照从小到大的顺序排列( ) ![]()
A.﹣b<﹣a<a<b
B.a<﹣b<b<﹣a
C.﹣b<a<﹣a<b
D.a<﹣b<﹣a<b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在3×3的方格纸中,点A,B,C,D,E分别位于如图所示的小正方形格点上.
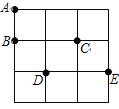
(1)在点A,B,C,D,E中任取四个点为顶点直接在图上画一个中心对称的四边形;
(2)从A,B,C三个点中先任取一个点,在余下的两个点中再取一个点,将所取的这两点与点D,E为顶点构成四边形,求所得四边形中面积为2的概率(用树状图或列表法求解).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在AC⊥BC,过点C的直线MN∥AB,D为AB边上一点,且AD=4,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求CE的长;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一张矩形纸片,剪下一个正方形,剩下一个矩形,称为第一次操作;在剩下的矩形纸片中再剪下一个正方形,剩下一个矩形,称为第二次操作…若在第 n 次操作后,剩下的矩形为正方形,则称原矩形为n阶奇异矩形.如图1,矩形ABCD中,若AB=2,BC=6,则称矩形ABCD为2阶奇异矩形.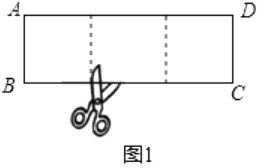
(1)判断与操作:
如图2,矩形ABCD的长为5,宽为2,它是奇异矩形吗?
如果是,请写出它是几阶奇异矩形,并在图中画出裁剪线;如果不是,请说明理由.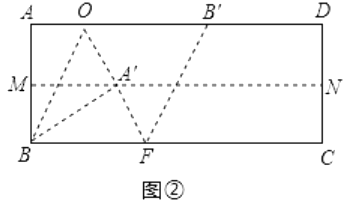
(2)探究与计算:
已知矩形ABCD的一边长为20,另一边长为a(a<20),且它是3阶奇异矩形,请画出矩形ABCD及裁剪线的示意图,并在图的下方写出a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com