
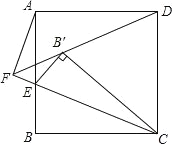
【题目】如图,E为正方形ABCD边AB上的一点,且AB=3,BE=1.将△CBE翻折得到△CB'E,连接并延长DB'与CE延长线相交于点F,连接AF,则AF的长为_____.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】(本小题满分10分)如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() 为常数,且
为常数,且![]() )的图象交于A(1,a)、B两点.
)的图象交于A(1,a)、B两点.
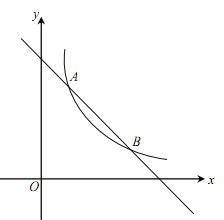
(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
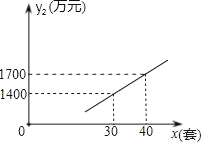
【题目】国家推行“节能减排,低碳经济”政策后,某环保节能设备生产企业的产品供不应求,若该企业的某种环保设备每月的产量保持在一定的范国,每套产品的售价不低于90万元,生产总成本不高于1250万元,已知这种设备的月产量x(套)与每套产品的售价y1(万元)之间满足关系式y1=130﹣x,月产量x(套)与生产总成本y2(万元)存在如图所示的函数关系.
(1)求出y2与x之间的函数关系式,并求月产量x的范围;
(2)当月产量x(套)为多少时,这种设备的利润W(万元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
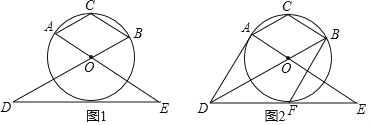
【题目】如图1,AOBC的顶点A、B、C在⊙O上,点D、E分别在BO、AO的延长线上,且OD=2OB,OE=2OA,连接DE.
(1)求∠AOB的度数;
(2)求证:DE是⊙O的切线;
(3)如图2,设直线DE与⊙O相切于点F,连接AD、BF,判断线段AD与BF的位置关系和数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠ABC=90°,AB=BC.点D是线段AC上一点,连接BD.过点C作CE⊥BD于点E.点F是AB垂直平分线上一点,连接BF、EF.
(1)若AD=4![]() ,tan∠BCE=
,tan∠BCE=![]() ,求AB的长;
,求AB的长;
(2)当点F在AC边上时,求证:∠FEC=45°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AC平分∠DAB,AC2=ABAD,∠ADC=90°,点E为AB的中点.
(1)求证:△ADC∽△ACB.
(2)若AD=2,AB=3,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
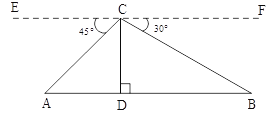
【题目】如图,从热气球C处测得地面A、B两点的俯角分别为45°、30°,如果此时热气球C处离地面的高度CD为100米,且点A、D、B在同一直线上,求AB两点间的距离(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD.
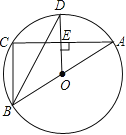
(1)求证:BD平分∠ABC;
(2) 当∠ODB=30°时,求证:BC=OD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com