
【题目】(1)解方程:4x(2x+1)=3(2x+1),
(2)用配方法解方程:x2+6x﹣40=0
【答案】(1)x1=﹣![]() ,x2=
,x2=![]() ;(2)x1=4,x2=﹣10.
;(2)x1=4,x2=﹣10.
【解析】
(1)观察方程等号两边的特征,可以选择提公因式法对方程进行因式分解,然后再根据解两个一元一次方程,(2)先将常数项移动到等号的右边,然后在方程两边同时加上一次项系数一半的平方,等号左边整理成完全平方形式,等号右边是常数,再根据平方根的意义开平方,最后求解.
(1)4x(2x+1)=3(2x+1),
4x(2x+1)﹣3(2x+1)=0,
(2x+1)(4x﹣3)=0,
2x+1=0,4x﹣3=0,
解得:x1=![]() ,x2=
,x2=![]() ;
;
(2)x2+6x﹣40=0,
x2+6x=40,
x2+6x+9=40+9,
(x+3)2=49,
x+3=±7,
解得:x1=4,x2=﹣10.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,⊿ABC中,AB=AC,以AB为直径的⊙O交BC于点P,PD⊥AC于点D.
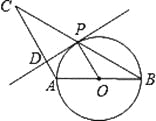
(1)求证:PD是⊙O的切线.
(2)若∠CAB=120°,AB=2,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调查:每个玩具按![]() 元销售时,每天可销售
元销售时,每天可销售![]() 个;若销售单价每降低元,每天可多售出
个;若销售单价每降低元,每天可多售出![]() 个.已知每个玩具的固定成本为
个.已知每个玩具的固定成本为![]() 元,问这种玩具的销售单价为多少元时,厂家每天可获利润
元,问这种玩具的销售单价为多少元时,厂家每天可获利润![]() 元?
元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列一元二次方程两实数根和为﹣4的是( )
A. x2+2x﹣4=0 B. x2﹣4x+4=0 C. x2+4x+10=0 D. x2+4x﹣5=0
查看答案和解析>>
科目:初中数学 来源: 题型:
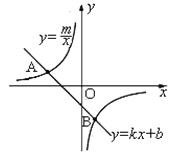
【题目】如题图,已知A(-4,2),B(n,-4)是一次函数y=kx+b的图象和反比例函数![]() 的图象的两个交点.
的图象的两个交点.
(1)求m,n的值;
(2)求一次函数的关系式;、
(3)结合图象直接写出一次函数小于反比例函数的x的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
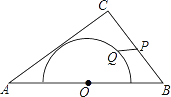
【题目】如图,在△ABC中,AB=5,AC=4,BC=3,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的和是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
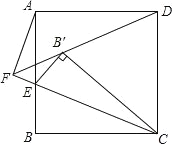
【题目】如图,E为正方形ABCD边AB上的一点,且AB=3,BE=1.将△CBE翻折得到△CB'E,连接并延长DB'与CE延长线相交于点F,连接AF,则AF的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
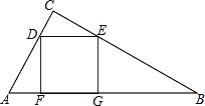
【题目】如图,已知△ABC中,四边形DEGF为正方形,D、E在线段AC、BC上,F、G在AB上,如果S△ADF=S△CDE=1,S△BEG=3,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com