
【题目】如图,已知△ABC中,四边形DEGF为正方形,D、E在线段AC、BC上,F、G在AB上,如果S△ADF=S△CDE=1,S△BEG=3,求△ABC的面积.
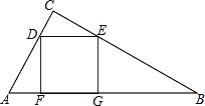
【答案】S△ABC=9.
【解析】
过C作CH⊥AB于H,交DE于M,设AF=a,正方形DFGE的边长为b,CM=h,由于S△CDE=![]() bh=1,S△AFD=
bh=1,S△AFD=![]() ab=1,于是得到a=h,CH=h+b=a+b,根据S△BEG=
ab=1,于是得到a=h,CH=h+b=a+b,根据S△BEG=![]() BGb=3,得到GB=3a,于是求出S△ABC=
BGb=3,得到GB=3a,于是求出S△ABC=![]() ABCH=
ABCH=![]() (a+b+3a)(a+b)=b2+5,由于ab=2,于是求得2a2+
(a+b+3a)(a+b)=b2+5,由于ab=2,于是求得2a2+![]() b2=b2,通过化简即可得到结论.
b2=b2,通过化简即可得到结论.
解:过C作CH⊥AB于H,交DE于M,
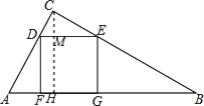
设AF=a,正方形DFGE的边长为b,CM=h,
∴S△CDE= ![]() bh=1,S△AFD=
bh=1,S△AFD= ![]() ab=1,
ab=1,
∴a=h,
∴CH=h+b=a+b,
∵S△BEG= ![]() BGb=3,
BGb=3,
∴GB=3a,
∴S△ABC= ![]() ABCH=
ABCH=![]() (a+b+3a)(a+b)=b2+5,
(a+b+3a)(a+b)=b2+5,
∵ab=2,
∴2a2+ ![]() b2=b2,
b2=b2,
∴b=2a,
∴![]() b×b=2,
b×b=2,
∴b2=4,
∴S△ABC=b2+5=9.


科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AC平分∠DAB,AC2=ABAD,∠ADC=90°,点E为AB的中点.
(1)求证:△ADC∽△ACB.
(2)若AD=2,AB=3,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
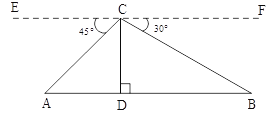
【题目】如图,从热气球C处测得地面A、B两点的俯角分别为45°、30°,如果此时热气球C处离地面的高度CD为100米,且点A、D、B在同一直线上,求AB两点间的距离(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为反比例函数y=![]() 的图像上一点,PA⊥x轴于点A,△PAO的面积为6,则下列各点中也在这个反比例函数图像上的是( )
的图像上一点,PA⊥x轴于点A,△PAO的面积为6,则下列各点中也在这个反比例函数图像上的是( )

A. (2,3) B. (﹣2,6) C. (2,6) D. (﹣2,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处距离灯塔P有多远?(结果用非特殊角的三角函数表示即可)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E,D,交OA于点F,连接EF并延长EF交AB于G,且EG⊥AB.
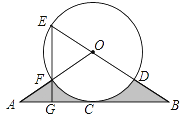
(1)求证:直线AB是⊙O的切线;
(2)若EF=2FG,AB= ![]() ,求图中阴影部分的面积;
,求图中阴影部分的面积;
(3)若EG=9,BG=12,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD.
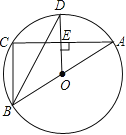
(1)求证:BD平分∠ABC;
(2) 当∠ODB=30°时,求证:BC=OD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系y=mx2+20x+n,其图象如图所示.
(1)m=_____,n=_____.
(2)销售单价为多少元时,该种商品每天的销售利润最大?最大利润为多少元?
(3)该种商品每天的销售利润不低于16元时,直接写出x的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com