
【题目】如图,P为反比例函数y=![]() 的图像上一点,PA⊥x轴于点A,△PAO的面积为6,则下列各点中也在这个反比例函数图像上的是( )
的图像上一点,PA⊥x轴于点A,△PAO的面积为6,则下列各点中也在这个反比例函数图像上的是( )

A. (2,3) B. (﹣2,6) C. (2,6) D. (﹣2,3)
科目:初中数学 来源: 题型:
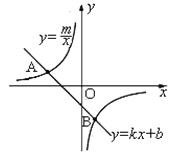
【题目】如题图,已知A(-4,2),B(n,-4)是一次函数y=kx+b的图象和反比例函数![]() 的图象的两个交点.
的图象的两个交点.
(1)求m,n的值;
(2)求一次函数的关系式;、
(3)结合图象直接写出一次函数小于反比例函数的x的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆O通过五边形OABCD的四个顶点.若弧ABD=150°,∠A=65°,∠D=60°,则弧BC的度数为何?( )
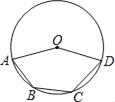
A. 25 B. 40 C. 50 D. 55
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣![]() x2﹣(m+3)x+m2﹣12与x轴交于A(x1,0)、B(x2,0)两点,且x1<0,x2>0,抛物线与y轴交于点C,OB=2OA.
x2﹣(m+3)x+m2﹣12与x轴交于A(x1,0)、B(x2,0)两点,且x1<0,x2>0,抛物线与y轴交于点C,OB=2OA.
(1)求抛物线解析式;
(2)已知直线y=![]() x+2与抛物线相交于M、N两点,分别过M、N作x轴的垂线,垂足为M1、N1,是否存在点P,同时满足如下两个条件:
x+2与抛物线相交于M、N两点,分别过M、N作x轴的垂线,垂足为M1、N1,是否存在点P,同时满足如下两个条件:
①P为抛物线上的点,且在直线MN上方;
②![]() :
:![]() =6:35
=6:35
若存在,则求点P横坐标t,若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两市相距150千米,分别从A、B处测得国家级风景区中心C处的方位角如图所示,风景区区域是以C为圆心,45千米为半径的圆,tanα=1.627,tanβ=1.373.为了开发旅游,有关部门设计修建连接AB两市的高速公路.问连接AB高速公路是否穿过风景区,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
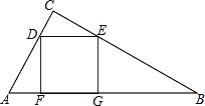
【题目】如图,已知△ABC中,四边形DEGF为正方形,D、E在线段AC、BC上,F、G在AB上,如果S△ADF=S△CDE=1,S△BEG=3,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在航线l的两侧分别有观测点A和B,点B到航线l的距离BD为4km,点A位于点B北偏西60°方向且与B相距20km处.现有一艘轮船从位于点A南偏东74°方向的C处,沿该航线自东向西航行至观测点A的正南方向E处.求这艘轮船的航行路程CE的长度.(结果精确到0.1km)(参考数据:![]() ≈1.73,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49)
≈1.73,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49)

查看答案和解析>>
科目:初中数学 来源: 题型:
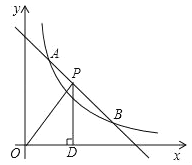
【题目】如图,一次函数y=﹣x+b与反比例函数![]() (x>0)的图象交于点A(m,3)和B(3,1).
(x>0)的图象交于点A(m,3)和B(3,1).
(1)填空:一次函数的解析式为 ,反比例函数的解析式为 ;
(2)点P是线段AB上一点,过点P作PD⊥x轴于点D,连接OP,若△POD的面积为S,求S的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com