
【题目】如图,圆O通过五边形OABCD的四个顶点.若弧ABD=150°,∠A=65°,∠D=60°,则弧BC的度数为何?( )
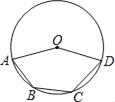
A. 25 B. 40 C. 50 D. 55
【答案】B
【解析】
连接OB,OC,由半径相等得到三角形OAB,三角形OBC,三角形OCD都为等腰三角形,根据∠A=65°,∠D=60°,求出∠1与∠2的度数,根据![]() 的度数确定出∠AOD度数,进而求出∠3的度数,即可确定出
的度数确定出∠AOD度数,进而求出∠3的度数,即可确定出![]() 的度数.
的度数.
连接OB、OC,
∵OA=OB=OC=OD,
∴△OAB、△OBC、△OCD,皆为等腰三角形,
∵∠A=65°,∠D=60°,
∴∠1=180°﹣2∠A=180°﹣2×65°=50°,∠2=180°﹣2∠D=180°﹣2×60°=60°,
∵![]() =150°,
=150°,
∴∠AOD=150°,
∴∠3=∠AOD﹣∠1﹣∠2=150°﹣50°﹣60°=40°,
则![]() 的度数为40°.
的度数为40°.
故选:B.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知有一块等腰三角形纸板,在它的两腰上各有一点E和F,把这两点分别与底边中点连结,并沿着这两条线段剪下两个三角形,所得的这两个三角形相似,剩余部分(四边形)的四条边的长度如图所示,那么原等腰三角形的底边长为( )

A. ![]() B.
B. ![]() C.
C. ![]() 或
或![]() D.
D. ![]() 或
或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,O为对角线BD的中点,EF经过点O分别交AD、BC于E、F两点,
(1)如图1,求证:AE=CF;
(2)如图2,若EF⊥BD,∠AEB=60°,请你直接写出与DE(DE除外)相等的所有线段.
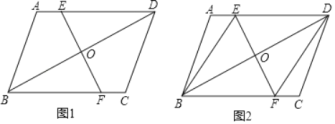
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AOBC的顶点A、B、C在⊙O上,点D、E分别在BO、AO的延长线上,且OD=2OB,OE=2OA,连接DE.
(1)求∠AOB的度数;
(2)求证:DE是⊙O的切线;
(3)如图2,设直线DE与⊙O相切于点F,连接AD、BF,判断线段AD与BF的位置关系和数量关系,并证明你的结论.
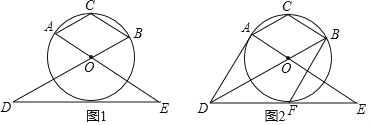
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系中,正比例函数y=x的图象与反比例函数y=![]() (k≠0)的图象交于点A(﹣2,﹣2),其中将直线OA向上平移3个单位后与y轴交于点C,与反比例函数在第三象限内交点为B(﹣4,m).
(k≠0)的图象交于点A(﹣2,﹣2),其中将直线OA向上平移3个单位后与y轴交于点C,与反比例函数在第三象限内交点为B(﹣4,m).
(1)求该反比例函数的解析式与平移后的直线解析式;
(2)求△ABC的面积.
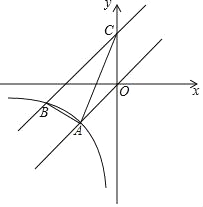
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AC平分∠DAB,AC2=ABAD,∠ADC=90°,点E为AB的中点.
(1)求证:△ADC∽△ACB.
(2)若AD=2,AB=3,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A、B两点的坐标分别为A(0,2![]() ),B(2,0),直线AB与反比例函数y=
),B(2,0),直线AB与反比例函数y=![]() 的图象相交于点C和点D,将△OBC绕点O逆时针方向旋转θ角(θ为锐角),得到△OB′C′,当θ=_____时,OC′⊥AB;
的图象相交于点C和点D,将△OBC绕点O逆时针方向旋转θ角(θ为锐角),得到△OB′C′,当θ=_____时,OC′⊥AB;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为反比例函数y=![]() 的图像上一点,PA⊥x轴于点A,△PAO的面积为6,则下列各点中也在这个反比例函数图像上的是( )
的图像上一点,PA⊥x轴于点A,△PAO的面积为6,则下列各点中也在这个反比例函数图像上的是( )

A. (2,3) B. (﹣2,6) C. (2,6) D. (﹣2,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
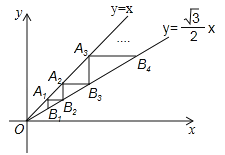
【题目】(2017辽宁省盘锦市,第18题,3分)如图,点A1(1,1)在直线y=x上,过点A1分别作y轴、x轴的平行线交直线![]() 于点B1,B2,过点B2作y轴的平行线交直线y=x于点A2,过点A2作x轴的平行线交直线
于点B1,B2,过点B2作y轴的平行线交直线y=x于点A2,过点A2作x轴的平行线交直线![]() 于点B3,…,按照此规律进行下去,则点An的横坐标为______.
于点B3,…,按照此规律进行下去,则点An的横坐标为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com