
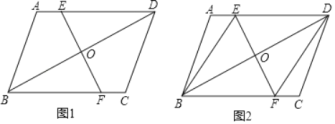
【题目】在平行四边形ABCD中,O为对角线BD的中点,EF经过点O分别交AD、BC于E、F两点,
(1)如图1,求证:AE=CF;
(2)如图2,若EF⊥BD,∠AEB=60°,请你直接写出与DE(DE除外)相等的所有线段.
【答案】(1)证明见解析;(2)BE、BF、EF、DF.
【解析】
(1)根据平行四边形的性质以及全等三角形的判定方法证明出△EOD≌△FOB,得到DE=BF,可得结论:
(2)由(1)OE=OF,而利用对角线互相垂直的平行四边形是菱形得出四边形BFDE为菱形,由∠AEB=60°可得△BEF与△BEF为等边三角形,从而得到结论.
(1)证明:![]() 四边形ABCD是平行四边形, BD为平行四边形ABCD对角线BD
四边形ABCD是平行四边形, BD为平行四边形ABCD对角线BD
![]() AD//BC,AD=BC,OB=OD.
AD//BC,AD=BC,OB=OD.
![]() ∠OED=∠OFB, ∠EDO=∠FBO.
∠OED=∠OFB, ∠EDO=∠FBO.
在△EOD与△FOB中,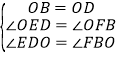 ,
,
![]() △EOD≌△FOB
△EOD≌△FOB
![]() ED=BF,
ED=BF,
又![]() AD=BC
AD=BC
![]() AE=CF.
AE=CF.
(2)由(1)得△EOD≌△FOB
![]() OE=OF,
OE=OF,
由![]() OB=OD,EF⊥BD
OB=OD,EF⊥BD
![]() 四边形BFDE为菱形,
四边形BFDE为菱形,
![]() ∠AEB=60°,
∠AEB=60°,![]() ∠BED=120°,且四边形BFDE为菱形,
∠BED=120°,且四边形BFDE为菱形,
![]() ∠BEF=∠DEF=60°,
∠BEF=∠DEF=60°, ![]() △BEF与△BEF为等边三角形,
△BEF与△BEF为等边三角形,
![]() 与DE相等的所有线段为:BE、BF、EF、DF.
与DE相等的所有线段为:BE、BF、EF、DF.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】已知抛一枚均匀硬币正面朝上的概率为![]() ,下列说法错误的是
,下列说法错误的是
A. 连续抛一均匀硬币2次必有1次正面朝上
B. 连续抛一均匀硬币10次都可能正面朝上
C. 大量反复抛一均匀硬币,平均100次出现正面朝上50次
D. 通过抛一均匀硬币确定谁先发球的比赛规则是公平的
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=2,点E在边AD上,∠ABE=45°,BE=DE,连接BD,点P在线段DE上,过点P作PQ∥BD交BE于点Q,连接QD.设PD=x,△PQD的面积为y,则能表示y与x函数关系的图象大致是( )


查看答案和解析>>
科目:初中数学 来源: 题型:
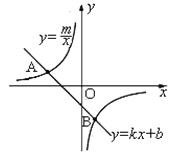
【题目】如题图,已知A(-4,2),B(n,-4)是一次函数y=kx+b的图象和反比例函数![]() 的图象的两个交点.
的图象的两个交点.
(1)求m,n的值;
(2)求一次函数的关系式;、
(3)结合图象直接写出一次函数小于反比例函数的x的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B两地相距4km,上午8:00时,亮亮从A地步行到B地,8:20时芳芳从B地出发骑自行车到A地,亮亮和芳芳两人离A地的距离S(km)与亮亮所用时间t(min)之间的函数关系如图所示,芳芳到达A地时间为( )
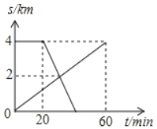
A. 8:30 B. 8:35 C. 8:40 D. 8:45
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=5,AC=4,BC=3,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的和是________.
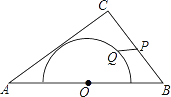
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们不妨约定:对角线互相垂直的凸四边形叫做“十字形”.
(1)在平行四边形、矩形、菱形、正方形中,一定是“十字形”的有 .
(2)如图1,在四边形ABCD中,AB=AD,且CB=CD
①证明:四边形ABCD是“十字形”;
②若AB=2.∠BAD=60°,∠BCD=90°,求四边形ABCD的面积.
(3)如图2.A、B、C、D是半径为1的⊙O上按逆时针方向排列的四个动点,AC与BD交于点E,若∠ADB﹣∠CDB=∠ABD﹣∠CBD.满足AC+BD=3,求线段OE的取值范围.
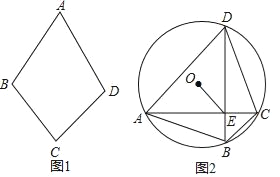
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆O通过五边形OABCD的四个顶点.若弧ABD=150°,∠A=65°,∠D=60°,则弧BC的度数为何?( )
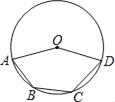
A. 25 B. 40 C. 50 D. 55
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在航线l的两侧分别有观测点A和B,点B到航线l的距离BD为4km,点A位于点B北偏西60°方向且与B相距20km处.现有一艘轮船从位于点A南偏东74°方向的C处,沿该航线自东向西航行至观测点A的正南方向E处.求这艘轮船的航行路程CE的长度.(结果精确到0.1km)(参考数据:![]() ≈1.73,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49)
≈1.73,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com