
����Ŀ�����Dz���Լ�����Խ����ഹֱ���ı��ν�����ʮ��������
��1����ƽ���ı��Ρ����Ρ����Ρ��������У�һ������ʮ������������ ����
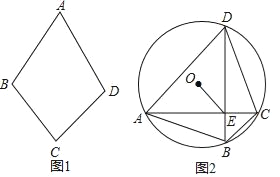
��2����ͼ1�����ı���ABCD�У�AB��AD����CB��CD
��֤�����ı���ABCD����ʮ��������
����AB��2����BAD��60�㣬��BCD��90�������ı���ABCD�������
��3����ͼ2��A��B��C��D�ǰ뾶Ϊ1�ġ�O�ϰ���ʱ�뷽�����е��ĸ����㣬AC��BD���ڵ�E������ADB����CDB����ABD����CBD������AC+BD��3�����߶�OE��ȡֵ��Χ��
���𰸡���1�����Ρ������Σ���2����֤�����������ڼ�������3��![]() ��OE��
��OE��![]() ��
��
��������
��1��������ʮ�������Ķ����жϼ��ɣ�
��2��������AC��BD�����ô�ֱƽ���ߵ��ж����ɣ�
�����жϳ���ADB+��CAD=��ABD+��CAB�������жϳ���AED=��AEB=90��������AC��BD�����жϳ��ı���OMEN�Ǿ��Σ������ó�OE2=2-��AC2+BD2������AC=m���г����κ����������ɣ�
��1����ƽ���ı��Ρ����Ρ����Ρ���������ֻ�����Ρ������εĶԽ����ഹֱ��
�ʴ�Ϊ�����Ρ������Σ�
��2������ͼ1������AC��BD
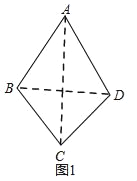
��AB��AD����CB��CD
��AC��BD�Ĵ�ֱƽ���ߣ�
��AC��BD��
���ı���ABCD����ʮ��������
����ͼ2
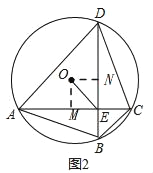
�ߡ�ADB+��CBD����ABD+��CDB����CBD����CDB����CAB��
���ADB+��CAD����ABD+��CAB��
��180������AED��180������AEB��
���AED����AEB��90����
��AC��BD��
����O��OM��AC��M��ON��BD��N������OA��OD��
��OA��OD��1��OM2��OA2��AM2��ON2��OD2��DN2��AM��![]() AC��DN��
AC��DN��![]() BD���ı���OMEN�Ǿ��Σ�
BD���ı���OMEN�Ǿ��Σ�
��ON��ME��OE2��OM2+ME2��
��OE2��OM2+ON2��2��![]() ��AC2+BD2��
��AC2+BD2��
��AC��m����BD��3��m��
�ߡ�O�İ뾶Ϊ1��AC+BD��3��
��1��m��2��
OE2��![]() ��
��
��![]() ��OE2��
��OE2��![]() ��
��
��![]() ��OE��
��OE��![]() .
.


 ѧ�ڸ�ϰһ��ͨѧϰ�ܶ�Ա��ĩ������ӱ����������ϵ�д�
ѧ�ڸ�ϰһ��ͨѧϰ�ܶ�Ա��ĩ������ӱ����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��O����ABΪֱ������ABC�����Բ������A����O�����߽�OC���ӳ����ڵ�D����BC���ӳ����ڵ�E��
��1����֤����DAC=��DCE��
��2����AB=2��sin��D=![]() ����AE�ij���
����AE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����y��4x2��4x+m��ͼ����x��Ľ�������Ϊ��x1��0������x2��0�����ң�x1+x2����4x12��5x1��x2����8����ú�������СֵΪ��������
A. 2 B. ��2 C. 10 D. ��10
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
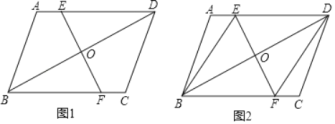
����Ŀ����ƽ���ı���ABCD�У�OΪ�Խ���BD���е㣬EF������O�ֱ�AD��BC��E��F���㣬
��1����ͼ1����֤��AE��CF��
��2����ͼ2����EF��BD����AEB��60�㣬����ֱ��д����DE��DE���⣩��ȵ������߶Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һԲ�ڽ����˱���ABCDEFGH������ADE�����Ϊ8�������˱���ABCDEFGH�����Ϊ��������
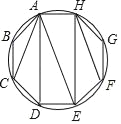
A. 32 B. 40 C. 24 D. 30
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
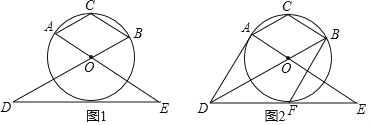
����Ŀ����ͼ1��AOBC�Ķ���A��B��C�ڡ�O�ϣ���D��E�ֱ���BO��AO���ӳ����ϣ���OD��2OB��OE��2OA������DE��
(1)���AOB�Ķ�����
(2)��֤��DE�ǡ�O�����ߣ�
(3)��ͼ2����ֱ��DE���O�����ڵ�F������AD��BF���ж��߶�AD��BF��λ�ù�ϵ��������ϵ����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
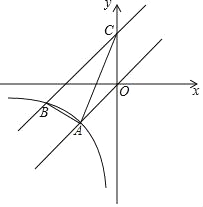
����Ŀ����֪����ͼ����ƽ��ֱ������ϵ�У�����������y��x��ͼ���뷴��������y��![]() ��k��0����ͼ���ڵ�A����2����2�������н�ֱ��OA����ƽ��3����λ����y�ύ�ڵ�C���뷴���������ڵ��������ڽ���ΪB����4��m����
��k��0����ͼ���ڵ�A����2����2�������н�ֱ��OA����ƽ��3����λ����y�ύ�ڵ�C���뷴���������ڵ��������ڽ���ΪB����4��m����
��1����÷����������Ľ���ʽ��ƽ�ƺ��ֱ�߽���ʽ��
��2�����ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪A��B���������ֱ�ΪA��0��2![]() ����B��2��0����ֱ��AB�뷴��������y��
����B��2��0����ֱ��AB�뷴��������y��![]() ��ͼ���ཻ�ڵ�C�͵�D������OBC�Ƶ�O��ʱ�뷽����ת�Ƚǣ���Ϊ��ǣ����õ���OB��C�䣬���ȣ�_____ʱ��OC���AB��
��ͼ���ཻ�ڵ�C�͵�D������OBC�Ƶ�O��ʱ�뷽����ת�Ƚǣ���Ϊ��ǣ����õ���OB��C�䣬���ȣ�_____ʱ��OC���AB��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=x2+bx+c��ͼ���㣨4��3������3��0����
��1����b��c��ֵ��
��2������ö��κ���ͼ��Ķ�������ͶԳ��ᣬ������������ϵ�л����ú�����ͼ����
��3���ú�����ͼ��������ƽ�Ƶõ�y=x2��ͼ����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com