
【题目】如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E,D,交OA于点F,连接EF并延长EF交AB于G,且EG⊥AB.
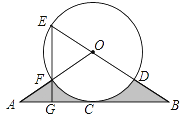
(1)求证:直线AB是⊙O的切线;
(2)若EF=2FG,AB= ![]() ,求图中阴影部分的面积;
,求图中阴影部分的面积;
(3)若EG=9,BG=12,求BD的长.
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)连接OE,由OA=OB,CA=CB,根据等腰三角形的性质得到OC⊥AB,根据切线的判定定理即可得到结论;
(2)过O点作OH⊥EG于H,则EH=FH,由EF=2FG,得到EH![]() EG,又OH∥BG,根据平行线分线段成比例定理得到EH:EG=EO:EB,BO=2OE,则OB=2OC,得到∠B=30°,而BC
EG,又OH∥BG,根据平行线分线段成比例定理得到EH:EG=EO:EB,BO=2OE,则OB=2OC,得到∠B=30°,而BC![]() AB=6
AB=6![]() ,利用含30°的直角三角形三边的关系得到OC
,利用含30°的直角三角形三边的关系得到OC![]() BC=6,然后根据三角形和扇形的面积公式利用S阴影部分=S△OAB﹣S扇形OFD计算即可;
BC=6,然后根据三角形和扇形的面积公式利用S阴影部分=S△OAB﹣S扇形OFD计算即可;
(3)利用勾股定理得到BE的长,设⊙O的半径为r,易证Rt△BOC∽Rt△BEG,由相似三角形的性质得到BC![]() r,BO
r,BO![]() r,则15﹣r
r,则15﹣r![]() r,求出r,利用BD=BE﹣ED计算即可.
r,求出r,利用BD=BE﹣ED计算即可.
(1)连接OC,如图,∵OA=OB,CA=CB,∴OC⊥AB,∴直线AB是⊙O的切线;
(2)过O点作OH⊥EG于H,如图,∵OE=OF,∴EH=FH.
∵EF=2FG,∴EH![]() EG,而EG⊥AB,∴OH∥BG,∴EH:EG=EO:EB,∴BO=2OE,∴OB=2OC,∴∠B=30°,∠COB=60°.
EG,而EG⊥AB,∴OH∥BG,∴EH:EG=EO:EB,∴BO=2OE,∴OB=2OC,∴∠B=30°,∠COB=60°.
而BC![]() AB=6
AB=6![]() ,∴OC
,∴OC![]() BC=6,∴S阴影部分=S△OAB﹣S扇形OFD
BC=6,∴S阴影部分=S△OAB﹣S扇形OFD![]() 12
12![]() 6
6![]() =36
=36![]() 12π;
12π;
(3)在Rt△BEG中,EG=9,BG=12,∴BE![]() 15,设⊙O的半径为r,则OB=15﹣r.
15,设⊙O的半径为r,则OB=15﹣r.
∵OC∥EG,∴Rt△BOC∽Rt△BEG,∴OC:EG=BC:BG=BO:BE,即r:9=BC:12=BO:15,∴BC![]() r,BO
r,BO![]() r,∴15﹣r
r,∴15﹣r![]() r,解得:r
r,解得:r![]() ,∴BD=BE﹣ED=15﹣2
,∴BD=BE﹣ED=15﹣2![]() .
.


科目:初中数学 来源: 题型:
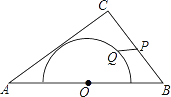
【题目】如图,在△ABC中,AB=5,AC=4,BC=3,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的和是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣![]() x2﹣(m+3)x+m2﹣12与x轴交于A(x1,0)、B(x2,0)两点,且x1<0,x2>0,抛物线与y轴交于点C,OB=2OA.
x2﹣(m+3)x+m2﹣12与x轴交于A(x1,0)、B(x2,0)两点,且x1<0,x2>0,抛物线与y轴交于点C,OB=2OA.
(1)求抛物线解析式;
(2)已知直线y=![]() x+2与抛物线相交于M、N两点,分别过M、N作x轴的垂线,垂足为M1、N1,是否存在点P,同时满足如下两个条件:
x+2与抛物线相交于M、N两点,分别过M、N作x轴的垂线,垂足为M1、N1,是否存在点P,同时满足如下两个条件:
①P为抛物线上的点,且在直线MN上方;
②![]() :
:![]() =6:35
=6:35
若存在,则求点P横坐标t,若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
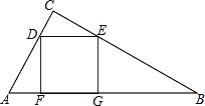
【题目】如图,已知△ABC中,四边形DEGF为正方形,D、E在线段AC、BC上,F、G在AB上,如果S△ADF=S△CDE=1,S△BEG=3,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在航线l的两侧分别有观测点A和B,点B到航线l的距离BD为4km,点A位于点B北偏西60°方向且与B相距20km处.现有一艘轮船从位于点A南偏东74°方向的C处,沿该航线自东向西航行至观测点A的正南方向E处.求这艘轮船的航行路程CE的长度.(结果精确到0.1km)(参考数据:![]() ≈1.73,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49)
≈1.73,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了能以“更新、更绿、更洁、更宁”的城市形象迎接2011年大运会的召开,深圳市全面实施市容市貌环境提升行动.某工程队承担了一段长为1500米的道路绿化工程,施工时有两张绿化方案:甲方案是绿化1米的道路需要A型花2枝和B型花3枝,成本是22元;乙方案是绿化1米的道路需要A型花1枝和B型花5枝,成本是25元.现要求按照乙方案绿化道路的总长度不能少于按甲方案绿化道路的总长度的2倍.
(1)求A型花和B型花每枝的成本分别是多少元?
(2)求当按甲方案绿化的道路总长度为多少米时,所需工程的总成本最少?总成本最少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
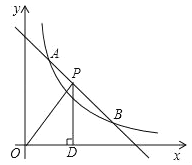
【题目】如图,一次函数y=﹣x+b与反比例函数![]() (x>0)的图象交于点A(m,3)和B(3,1).
(x>0)的图象交于点A(m,3)和B(3,1).
(1)填空:一次函数的解析式为 ,反比例函数的解析式为 ;
(2)点P是线段AB上一点,过点P作PD⊥x轴于点D,连接OP,若△POD的面积为S,求S的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不正确的是
A. 某种彩票中奖的概率是![]() ,买1000张该种彩票一定会中奖
,买1000张该种彩票一定会中奖
B. 了解一批电视机的使用寿命适合用抽样调查
C. 若甲组数据的标准差S甲=0.31,乙组数据的标准差S乙=0.25,则乙组数据比甲组数据稳定
D. 在一个装有白球和绿球的袋中摸球,摸出黑球是不可能事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,每个小正方形的边长都是1的方格纸中,有线段AC和EF,点A、C、E、F都在小正方形的顶点上.
(1)在方格纸中画出一个以线段AC为对角线的正方形ABCD,所画的正方形的各顶点必须在小正方形的顶点上.
(2)在方格纸中以EF为腰画出等腰三角形△EFM,点M在小正方形的顶点上,且MF=MC.
(3)在(1)、(2)的条件下,连接MA,请直接写出线段MA的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com