
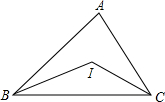
 如图,已知点I为△ABC外心,且∠BIC=150°,则∠A=75°.
如图,已知点I为△ABC外心,且∠BIC=150°,则∠A=75°. 科目:初中数学 来源: 题型:填空题
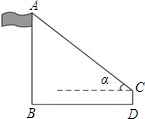 如图,用测倾仪测得校园内旗杆顶点A的仰角α=45°,仪器高CD=1.2m,测倾仪底部中心位置D到旗杆根部B的距离DB=9.8m,这时旗杆AB的高为11 m.
如图,用测倾仪测得校园内旗杆顶点A的仰角α=45°,仪器高CD=1.2m,测倾仪底部中心位置D到旗杆根部B的距离DB=9.8m,这时旗杆AB的高为11 m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
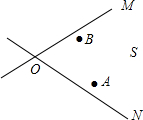 如图,学校要在两条小路OM和ON之间的S区域规划修建一处“英语角”,按照设计要求,英语角C到两栋教学楼A,B的距离必须相等,到两条小路的距离也必须相等,则“英语角”应修建在什么位置?请在图上标出它的位置.(尺规作图,保留痕迹)
如图,学校要在两条小路OM和ON之间的S区域规划修建一处“英语角”,按照设计要求,英语角C到两栋教学楼A,B的距离必须相等,到两条小路的距离也必须相等,则“英语角”应修建在什么位置?请在图上标出它的位置.(尺规作图,保留痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 定义:对于抛物线y=ax2+bx+c(a、b、c是常数,a≠0),若b2=ac,则称该抛物线为黄金抛物线.例如:y=2x2-2x+2是黄金抛物线.
定义:对于抛物线y=ax2+bx+c(a、b、c是常数,a≠0),若b2=ac,则称该抛物线为黄金抛物线.例如:y=2x2-2x+2是黄金抛物线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
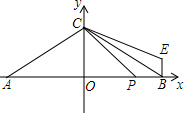 已知如图,A(-4,0)、C(0,4),点B在x轴正半轴上,AC=BC,D点坐标为(3,0),连接CD,将△BCD沿直线BC折,E点为D点的对应点.
已知如图,A(-4,0)、C(0,4),点B在x轴正半轴上,AC=BC,D点坐标为(3,0),连接CD,将△BCD沿直线BC折,E点为D点的对应点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 互补的两个角一定不相等 | B. | 相等的两个角是对顶角 | ||
| C. | 有公共顶点的两个角是对顶角 | D. | 同角(或等角)的余角相等,补角相等 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com