
����Ŀ����1���Ķ����ش�
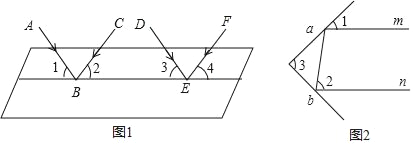
��ѧʵ��֤����ƽ�澵������ߵĹ����ǣ��䵽ƽ�澵�ϵĹ��ߺͱ�������Ĺ�����ƽ�澵���еĽ���ȣ���ͼ1��һ��ƽ�й���AB��DE����һ��ˮƽ������䣬��ʱ��1=��2����3=��4��
��������֪����1����3�Ĵ�С��ϵ���� ������������ ������2����4�Ĵ�С��ϵ���� ����
�������BC��EF��λ�ù�ϵ���� ������������ ����
��2��������⣺
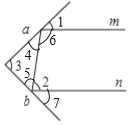
����ͼ2��һ������m�䵽ƽ�澵a�ϣ���a���䵽ƽ�澵b�ϣ��ֱ�b�����䣬��b������Ĺ���nƽ����m������1=35��������2=�� ������3=�� ����
����������1=40��������3=�� ����
���٢�������룺����3=�� ��ʱ���κ��䵽ƽ�澵a�ϵĹ���m����ƽ�澵a��b�����η�����������m�뷴�����n����ƽ�еģ���˵�����ɣ�
���𰸡���1������ȡ���ֱ��ƽ�У�ͬλ����ȡ���ȣ���ƽ�С�ͬλ����ȣ���ֱ��ƽ�У���2����70�㡢90�㣻��90�㣻��90�㣮
��������
��1������ƽ���ߵ��ж���������һ��⣻
��2���ٸ�������ǵ��ڷ���ǵó���1=��4����5=��7�������6������ƽ�������ʼ��������2�������5�������������ڽǺ������3���ɣ�
�����ͬ����
�������4+��5�������1+��4+��5+��7�����������2+��6������ƽ���ߵ��ж��Ƴ����ɣ�
��1������������֪����1����3�Ĵ�С��ϵ����ȣ���������ֱ��ƽ�У�ͬλ����ȣ���2����4�Ĵ�С��ϵ����ȣ�
���������BC��EF��λ�ù�ϵ��ƽ�У�������ͬλ����ȣ���ֱ��ƽ�У�
�ʴ�Ϊ������ȡ���ֱ��ƽ�У�ͬλ����ȡ���ȣ���ƽ�С�ͬλ����ȣ���ֱ��ƽ�У�
��2������ͼ��
�ߡ�1=35�㣬
���4=��1=35�㣬
���6=180�㩁35�㩁35��=110�㣬
��m��n��
���2+��6=180�㣬
���2=70�㣬
���5=��7=55�㣬
���3=180�㩁55�㩁35��=90�㣻
�������У�����1=40��������4=��1=40�㣬
���6=180�㩁40�㩁40��=100�㣬
��m��n��
���2+��6=180�㣬
���2=80�㣬
���5=��7=50�㣬
���3=180�㩁50�㩁40��=90��.
�����룺����3=90��ʱ��m��ƽ����n��
���ɣ��������ε��ڽǺ�Ϊ180��������3=90�㣬

���4+��5=90��.
�ߡ�4=��1����5=��7��
���1+��7=90�㣬
���1+��4+��5+��7=90��+90��=180�㣬
�ߡ�1+��4+��6+��5+��2+��7=180��+180��=360�㣬
���6+��2=180��.
��m��n��ͬ���ڽǻ�������ֱ��ƽ�У�.
�ʴ�Ϊ����70�㡢90�㣻��90�㣻��90�㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
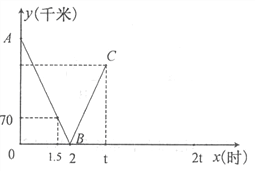
����Ŀ��һ���쳵�Ӽ�ʻ���ҵأ�һ���������ҵ�ʻ���أ�����ͬʱ������������ʻ.����ʻ��ʱ��Ϊx(ʱ)������֮��ľ���Ϊy(ǧ��)��ͼ�е����߱�ʾ�������������쳵�����ҵع�����y��x֮��ĺ�����ϵ������ͼ����Ϣ��
��1�����߶�AB����ֱ�ߵĺ�������ʽ��
��2�� ����ü�������֮��ľ���Ϊ ǧ�ף�
��3����֪��������ʱ�쳵����180ǧ�ף���쳵�Ӽص����ҵ�����ʱ��Ϊ Сʱ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��һ���ң���AB=4![]() �� ��C��E�ֱ��ڡ�O�ϣ���OC��AB�ڵ�D����E=30�㣬����OA��
�� ��C��E�ֱ��ڡ�O�ϣ���OC��AB�ڵ�D����E=30�㣬����OA��
��1����OA�ij���
��2����AF�ǡ�O����һ���ң��ҵ�O��AF�ľ���Ϊ2![]() �� ֱ��д����BAF�Ķ�����
�� ֱ��д����BAF�Ķ�����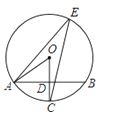
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ͼ������OEFPMN��������ij��������ʻ�������ٶ���ʱ��ĺ�����ϵ������˵���д�����ǣ� ��

A. ��3��ʱ�������ٶ���40ǧ��/ʱ
B. ��12��ʱ�������ٶ���0ǧ��/ʱ
C. �ӵ�3�ֵ���6�֣�������ʻ��120ǧ��
D. �ӵ�9�ֵ���12�֣��������ٶȴ�60ǧ��/ʱ���ٵ�0ǧ��/ʱ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ACB=90�㣬DΪAC��һ�㣬DE��AB�ڵ�E��AC=12��BC=5��
��1����cos��ADE��ֵ��
��2����DE=DCʱ����AD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AOB=45������M��N�ڱ�OA�ϣ�OM=3��ON=7����P��ֱ��OB�ϵĵ㣬Ҫʹ��P��M��N���ɵ��������εĵ�P�У�����������
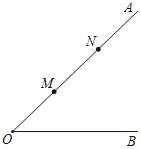
A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��߳�Ϊ2��������ABCD�ڵ�һ�����ڣ�AB��x�ᣬ��A������Ϊ��5��3������ֱ֪��l��y= ![]() x��2
x��2
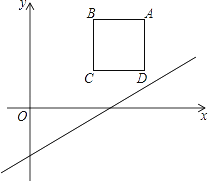
��1����ֱ��l����ƽ��m����λ��ʹƽ�ƺ��ֱ��ǡ�þ�����A����m��ֵ
��2���ڣ�1���������£�ƽ�ƺ��ֱ���������εı߳�BC���ڵ�E������ABE�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���P��y�������ڵ�C����P�İ뾶��4��ֱ��y=x����P�صõ���AB�ij�Ϊ4![]() �� ���P�����꣮
�� ���P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������������ǣ� ��
A. �����Խ�����ȵ��ı����Ǿ��Σ�
B. ��һ���Խ���ƽ��һ���ڽǵ�ƽ���ı���Ϊ���Σ�
C. �Խ����ഹֱ����ȵ��ı����������Σ�
D. ���������ı��θ��ߵ��е㣬�����ı��������Σ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com