
【题目】在平面直角坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“非常距离”,给出如下定义:
若|x1x2|≥|y1y2|,则点P1与点P2的“非常距离”为|x1x2|;
若|x1x2||y1y2|,则点P1与点P2的“非常距离”为|y1y2|.
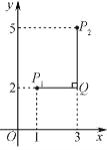
例如:点P1(1,2),点P2(3,5),因为|13||25|,所以点P1与点P2的“非常距离”为|25|3,也就是图中线段P1Q与线段P2Q长度的较大值(点Q为垂直于y轴的直线P1Q与垂直于x轴的直线P2Q的交点).
(1)已知点A(0,1),
①在B(![]() ,0),C(2,1),D(1,2),E(0,
,0),C(2,1),D(1,2),E(0,![]() )四个点中,与点A的“非常距离”为
)四个点中,与点A的“非常距离”为![]() 的点是;
的点是;
②点F为x轴上一动点,直接写出点A与点F的“非常距离”的最小值;
(2)已知点M是直线y2x6上的一个动点,
①点G的坐标是(0,2),求点M与点G的“非常距离”的最小值及相应的点M的坐标;
①点N是以点(4,0)为圆心,![]() 为半径的圆上的一个动点,直接写出点M与点N的“非常距离”的最小值及相应的点M的坐标.
为半径的圆上的一个动点,直接写出点M与点N的“非常距离”的最小值及相应的点M的坐标.
【答案】(1)①B ,E;②1; (2)①点 M 的坐标为(![]() ),②M 与点 N 的“非常距离”的最小值为 3,M(1, 4).
),②M 与点 N 的“非常距离”的最小值为 3,M(1, 4).
【解析】
(1)①由“非常距离”的定义可以确定在B(![]() ,0),C(2,1),D(1,2),E(0,
,0),C(2,1),D(1,2),E(0,![]() )四个点中,与点A的“非常距离”,据此可以得答案;
)四个点中,与点A的“非常距离”,据此可以得答案;
②设点F的坐标为(x,0),根据|0-x|<|0-1|,得出点F与点A的“非常距离”最小值为|0-1|=1,即可得出答案;
(2)①设点M的坐标为(x0,2x06),先确定出M点的位置,由M在直线y=2x+6上,设出M点坐标(x0,2x06),由条件可求得M点坐标及点M与点G的“非常距离”d的最小值及相应的点M的坐标;;
②当点P在过原点且与直线y=-2x-6垂直的直线上时,点M与点P的“非常距离”最小,利用相似求出P(2,1),进而求解即可.
解:
(1)①根据定义可得:
点A(0,1)与点B(![]() ,0)的“非常距离”为
,0)的“非常距离”为![]() =
=![]() ;
;
点A(0,1)与点C(2,1)的“非常距离”为![]() =2;
=2;
点A(0,1)与点D(-1,2)的“非常距离”为![]() =1;
=1;
点A(0,1)与点E(0,-![]() )的“非常距离”为
)的“非常距离”为![]() =
=![]() ;
;
故与点A的“非常距离”为![]() 的是B,E.
的是B,E.
(2)设点F的坐标为(x,0),若点F与点A的“非常距离”最小值,则|0-x|<|0-1|故为“非常距离”最小值|0-1|=1,
故答案为①B,E;②1;
(2)①过M点作y轴的垂线,垂足为点H,连结MG,当点M在点G的左上方且使△MGH为等腰直角三角形时,点M与点G的“非常距离”最小.
设点M的坐标为(x0,2x06),由HM=HN得
|x0-0|=|2x06-2|,解得:x0=-4,或x0=![]()
∴点M的坐标为(-4,-2)或(![]() ,
,![]() ),
),
∴HM=HN=4或![]() ,
,
∴点M与点N的“非常距离”的最小值为![]() ,相应的M的坐标为(
,相应的M的坐标为(![]() ,
,![]() );
);
②.当点N在过圆心P且与直线y=2x+6垂直的直线上时,点M与点N的“非常距离”最小,设N(x,y)(点N位于第一象限).过N点作NH⊥x轴,
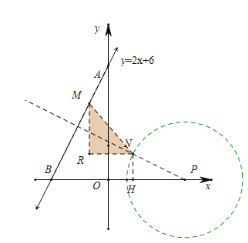
直线y=2x+6交坐标轴于A(0,6),B(-3,0),
∴AB=3![]() ,
,
∵△PBM∽△PNH,
∴![]()
∵PN=![]()
∴NH=1,PH=2,
∵P(4,0),
∴N(2,1),
当2-x02x061
∴x01
∴M(1,4),
点M与点N的“非常距离”的最小值为3.


科目:初中数学 来源: 题型:
【题目】如图1,一扇门ABCD,宽度AB=1m,A到墙角E的距离AE=0.5m,设E,A,B在一条直线上,门打开后被与门所在墙面垂直的墙阻挡(EA⊥EB′),边BC靠在墙B'C'的位置.
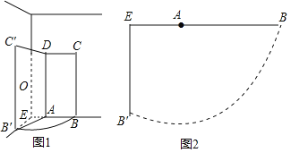
(1)求∠BAB'的度数;
(2)打开门后,门角上的点B在地面扫过的痕迹为弧BB',设弧BB'与两墙角线围成区域(如图2)的面积为S(m2),求S的值(π≈3.14,![]() ≈1.73,精确到0.1).
≈1.73,精确到0.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
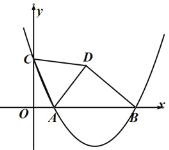
【题目】如图,在平面直角坐标系中,点C是y轴正半轴上的一个动点,抛物线y=ax2-6ax+5a(a是常数,且a>0)过点C,与x轴交于点A、B,点A在点B的左边.连接AC,以AC为边作等边三角形ACD,点D与点O在直线AC两侧,连接BD,则BD的最小值是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有![]() 个小球,它们除了颜色不同外,其余都相同, 其中有 5 个白球,每次试验前,将盒子中的小球摇匀,随机摸出一个球记下颜色后再放回盒中.下表是摸球试验的一组统计数据:
个小球,它们除了颜色不同外,其余都相同, 其中有 5 个白球,每次试验前,将盒子中的小球摇匀,随机摸出一个球记下颜色后再放回盒中.下表是摸球试验的一组统计数据:
摸球次数( n ) | 50 | 100 | 150 | 200 | 250 | 300 | 500 |
摸到白球次( m ) | 28 | 60 | 78 | 104 | 123 | 152 | 251 |
白球频率( | 0.56 | 0.60 | 0.52 | 0.52 | 0.49 | 0.51 | 0.50 |
由上表可以推算出a大约是( )
A.10B.14C.16D.40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB垂直于弦CD,垂足为点E,过点C作⊙O 的切线,交AB的延长线于点P,联结PD.
(1)判断直线PD与⊙O的位置关系,并加以证明;
(2)联结CO并延长交⊙O于点F,联结FP交CD于点G,如果CF=10,cos∠APC=![]() ,求EG的长.
,求EG的长.
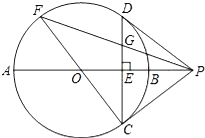
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某街道需要铺设管线的总长为9000![]() ,计划由甲队施工,每天完成150
,计划由甲队施工,每天完成150![]() .工作一段时间后,因为天气原因,想要40天完工,所以增加了乙队.如图表示剩余管线的长度
.工作一段时间后,因为天气原因,想要40天完工,所以增加了乙队.如图表示剩余管线的长度![]() 与甲队工作时间
与甲队工作时间![]() (天)之间的函数关系图象.
(天)之间的函数关系图象.
(1)直接写出点![]() 的坐标;
的坐标;
(2)求线段![]() 所对应的函数解析式,并写出自变量
所对应的函数解析式,并写出自变量![]() 的取值范围;
的取值范围;
(3)直接写出乙队工作25天后剩余管线的长度.
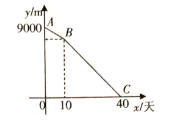
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】电子政务、数字经济、智慧社会……一场数字革命正在神州大地激荡,在第二届数字中国建设峰会召开之际,某校举行了第二届“掌握新技术,走进数时代”信息技术应用大赛,将该校八年级参加竞赛的学生成绩统计后,绘制成如下统计图表(不完整)
“掌握新技术,走进数时代”信息技术应用大赛成绩频数分布统计表:
组别 | 成绩x(分) | 人数 |
A | 60≤x<70 | 10 |
B | 70≤x<80 | m |
C | 80≤x<90 | 16 |
D | 90≤x≤100 | 4 |

请观察上面的图表,解答下列问题:
(1)统计表中m= ;统计图中n= ;B组的圆心角是 度.
(2)D组的4名学生中,有2名男生和2名女生.从D组随机抽取2名学生参加5G体验活动,请你画出树状图或用列表法求:
①恰好1名男生和1名女生被抽取参加5G体验活动的概率;
②至少1名女生被抽取参加5G体验活动的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解学生参加体育活动的情况,学校对学生进行随机抽样调查,其中一个问题是“你平均每天参加体育活动的时间是多少”,共有4个选项:A.1.5小时以上;B.1~1.5小时;C.0.5~1小时;D.0.5小时以下.图1、2是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息,解答以下问题:
(1)本次一共调查了多少名学生?
(2)在图1中将选项B的部分补充完整;
(3)若该校有3000名学生,你估计全校可能有多少名学生平均每天参加体育活动的时间在1小时以下.
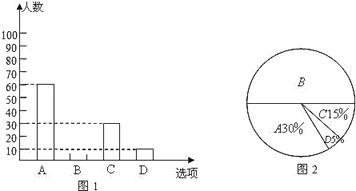
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (
(![]() 为常数),当自变量
为常数),当自变量![]() 的值满足
的值满足![]() 时,与其对应的函数值
时,与其对应的函数值![]() 的最大值为-1,则
的最大值为-1,则![]() 的值为( )
的值为( )
A. 3或6 B. 1或6 C. 1或3 D. 4或6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com