
����Ŀ��С����һ����ѧ��ȤС���У���һ����ѧ����������̽����
�����龳����ͼ1���ı���ABCD�У�AD��BC����EΪDC�ߵ��е㣬����AE���ӳ���BC���ӳ����ڵ�F����֤��S�ı���ABCD=S��ABF �� ��S��ʾ�����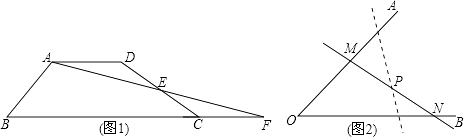
����Ǩ�ƣ���ͼ2������֪��ǡ�AOB����һ������P������P������һ��ֱ��MN���ֱ�����OA��OB�ڵ�M��N��С����ֱ��MN���ŵ�P��ת�Ĺ����з��֣���MON�����������Сֵ�����ʵ�ֱ��MN��ʲôλ��ʱ����MON�������С����˵�����ɣ�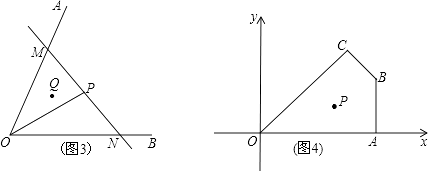
ʵ��Ӧ�ã���ͼ3�����ڵ�·OA��OB֮����һ��ׯQ�������飬���߲��żƻ��Թ�·OA��OB�;�������վP��һ��ֱ��MNΪ�����ߣ�����һ�������С�������θ�������MON������á�AOB=66�㣬��POB=30�㣬OP=4km�������MON��������������ȷ��0.1km2�����ο����ݣ�sin66���0.91��tan66���2.25�� ![]() ��1.73��
��1.73��
��չ���죺��ͼ4����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��A��B��C��P������ֱ�Ϊ��6��0����6��3���� ![]() ��
�� ![]() ������4��2��������p��ֱ��l���ı���OABCһ��Ա��ཻ�����ı���OABC�ֳ������ı��Σ��������Ե�OΪ������ı�����������ֵ��
������4��2��������p��ֱ��l���ı���OABCһ��Ա��ཻ�����ı���OABC�ֳ������ı��Σ��������Ե�OΪ������ı�����������ֵ��
���𰸡��⣺�����龳����AD��BC��
���DAE=��F����D=��FCE��
�ߵ�EΪDC�ߵ��е㣬
��DE=CE��
���ڡ�ADE�͡�FCE�У� ��
��
���ADE�ա�FCE��AAS����
��S��ADE=S��FCE ��
��S�ı���ABCE+S��ADE=S�ı���ABCE+S��FCE ��
��S�ı���ABCD=S��ABF��
����Ǩ�ƣ�����ֱ����ת����P��MN���е�ʱS��MON��С����ͼ2��
����P����һ��ֱ��EF��OA��OB�ڵ�E��F����PF��PE������M��MG��OB��EF��G��
�������龳���Եó���P��MN���е�ʱS�ı���MOFG=S��MON ��
��S�ı���MOFG��S��EOF ��
��S��MON��S��EOF ��
�൱��P��MN���е�ʱS��MON��С��
ʵ�����ã���ͼ3����PP1��OB��MM1��OB������ֱ�ΪP1 �� M1 ��
��Rt��OPP1��
�ߡ�POB=30�㣬
��PP1= ![]() OP=2��OP1=2
OP=2��OP1=2 ![]() ��
��
������Ǩ�ƵĽ���֪������PM=PNʱ����MON�������С��
��MM1=2PP1=4��M1P1=P1N��
��Rt��OMM1��
tan��AOB= ![]() ��
��
2.25= ![]() ��
��
��OM1= ![]() ��
��
��M1P1=P1N=2 ![]() ��
�� ![]() ��
��
��ON=OP1+P1N=2 ![]() +2
+2 ![]() ��
�� ![]() =4
=4 ![]() ��
�� ![]() ��
��
��S��MON= ![]() ONMM1=
ONMM1= ![]() ��4
��4 ![]() ��
�� ![]() ����4=8
����4=8 ![]() ��
�� ![]() ��10.3km2 ��
��10.3km2 ��
��չ���죺����ͼ4��������P��ֱ��l���ı���OABC��һ��Ա�OC��AB�ֱ��ڵ�M��N���ӳ�OC��AB���ڵ�D��
��C�� ![]() ��
�� ![]() ����
����
���AOC=45�㣬
��AO=AD��
��A��6��0����
��OA=6��
��AD=6��
��S��AOD= ![]() ��6��6=18��
��6��6=18��
������Ǩ�ƵĽ��ۿ�֪����PN=PMʱ����MND�������С��
���ı���ANMO��������
��PP1��OA��MM1��OA������ֱ�ΪP1 �� M1 ��
��M1P1=P1A=2��
��OM1=M1M=2��
��MN��OA��
��S�ı���OANM=S��OMM1+S�ı���ANMM1= ![]() ��2��2+2��4=10
��2��2+2��4=10
����ͼ5��������P��ֱ��l���ı���OABC����һ��Ա�CB��OA�ֱ�M��N���ӳ�CB��x����T��
��C�� ![]() ��
�� ![]() ����B��6��3������ֱ��BC�Ľ���ʽΪy=kx+b�������⣬��
����B��6��3������ֱ��BC�Ľ���ʽΪy=kx+b�������⣬�� ��
��
��ã� ![]() ��
��
��y=��x+9��
��y=0ʱ��x=9��
��T��9��0����
��S��OCT= ![]() 9=
9= ![]() ��
��
������Ǩ�ƵĽ��ۿ�֪����PM=PNʱ����MNT�������С��
���ı���CMNO��������
��NP1=M1P1 �� MM1=2PP1=4��
��4=��x+9��
��x=5��
��M��5��4����
��OM1=5��
��P��4��2����
��OP1=4��
��P1M1=NP1=1��
��ON=3��
��NT=6��
��S��MNT= ![]() ��4��6=12��
��4��6=12��
��S�ı���OCMN= ![]() ��12=
��12= ![]() ��10��
��10��
�������������ص��ı�����������ֵΪ10��


�������������龳�����ݿ�����á�ADE�ա�FCE���Ϳ��Եó�S��ADE=S��FCE�Ϳ��Եó����ۣ�
����Ǩ�ƣ����������龳�Ľ��ۿ��Եó���ֱ����ת����P��MN���е�ʱS��MON��С������M��MG��OB��EF��G����ȫ�������ε����ʿ��Եó����ۣ�
ʵ�����ã���ͼ3����PP1��OB��MM1��OB������ֱ�ΪP1 �� M1 �� �ٸ������������Ǻ���ֵ�Ϳ���������ۣ�
��չ���죺��������۵�����P��ֱ��l���ı���OABC��һ��Ա�OC��AB�ֱ��ڵ�M��N���ӳ�OC��AB���ڵ�D�����������Եó�AD=6���Ϳ��������OAD��������ٸ�������Ǩ�ƵĽ��۾Ϳ���������ֵ��
������P��ֱ��l���ı���OABC����һ��Ա�CB��OA�ֱ�M��N���ӳ�CB��x����T����B��C������ɵ�ֱ��BC�Ľ���ʽ���Ϳ������T�����꣬�Ӷ������OCT���������������Ǩ�ƵĽ��ۿ���������ֵ��ͨ���ȽϾͿ���������ۣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�ǡ�O���ڽ��ı��Σ���ABC=2��D������OA��OB��OC��AC��OB��AC�ཻ�ڵ�E������COB=3��AOB��OC=2 ![]() ����ͼ����Ӱ�������������������к��ţ�
����ͼ����Ӱ�������������������к��ţ� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���ݳ��Ӽص��ҵأ�����������xminʱ���ٶ�Ϊykm/h��ͼ�е����߱�ʾ���������ݳ�������y��x֮��ĺ�����ϵ�� 
��1��С���ݳ�������ٶ���km/h��
��2����20��x��30ʱ����y��x֮��ĺ�����ϵʽ�������С��������22minʱ���ٶȣ�
��3���������ÿ��ʻ100km����10L����ôС���ݳ��Ӽص��ҵع����Ͷ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ھ���ABCD�У�����A���۵��Խ���BD�ϵĵ�M�����ۺ�BE��AD�ڵ�E������C���۵��Խ���BD�ϵĵ�N�����ۺ�DF��BC�ڵ�F�� 
��1����֤���ı���BFDEΪƽ���ı��Σ�
��2�����ı���BFDEΪ���Σ���AB=2����BC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���B=90�㣬��A=30�㣬AC=2 ![]() ��
�� 
��1�����ó߹����߶�AC�Ĵ�ֱƽ����DE������ΪE����AB�ڵ�D����������ͼ�ۼ�����д������
��2������ADE���ܳ�Ϊa���Ȼ���T=��a+1��2��a��a��1��������T��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB�ǡ�O��ֱ������CD��AB�ڵ�E��G�� ![]() ���е㣬����AD��AG��CD�������н��۲�һ���������ǣ� ��
���е㣬����AD��AG��CD�������н��۲�һ���������ǣ� �� 
A.CE=DE
B.��ADG=��GAB
C.��AGD=��ADC
D.��GDC=��BAD
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ڽ��ڡ�O��ֱ��AFƽ�֡�BAC����BC�ڵ�D�� 
��1����ͼ1����֤��AB=AC��
��2����ͼ2���ӳ�BA����E������ED��EC��ED��AC�ڵ�G����ED=EC����֤����EGC=��ECA+2��ACB��
��3����ͼ3���ڣ�2���������£���BC�ǡ�O��ֱ��ʱ��ȡDC���е�M������AM���ӳ���Բ�ڵ�N����EG=5������CN����CN�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com