
分析 遇店加一倍,见花喝一斗,意思是碰到酒店把壶里的酒加1倍,碰到花就把壶里的酒喝一斗,三遇店和花,意思是每次都是遇到店后又遇到花,一共是3次,等量关系为:第一次加酒-1+(2×一遇店和花后剩的酒量-1)+(2×二遇店和花后剩的酒量-1)=0,依此列出方程即可.
解答 解:设壶中原来有酒x斗,他三遇店,同时也三见花.
第一次见店又见花后,酒有:2x-1;
第二次见店又见花后,酒有:2(2x-1)-1;
第三次见店又见花后,酒有:2[2(2x-1)-1]-1=0;
故答案为2[2(2x-1)-1]-1=0.
点评 本题考查了由实际问题抽象出一元一次方程,得到酒的数量为0的等量关系是解决本题的关键;难点是理解题意.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
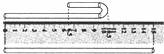 如图,直尺的下面是吸管的展直状态(最大长度),上面是该吸管的包装状态(外侧绷紧),弯曲部分可视为一半圆环,设其外圆半径为xcm,则根据题意可列方程为6.5+2(10.5-6.5-x)+πx=15.
如图,直尺的下面是吸管的展直状态(最大长度),上面是该吸管的包装状态(外侧绷紧),弯曲部分可视为一半圆环,设其外圆半径为xcm,则根据题意可列方程为6.5+2(10.5-6.5-x)+πx=15.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
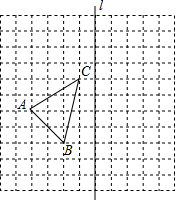 如图,在11×11的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
如图,在11×11的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com