
 如图,已知在矩形ABCD中,AD=10,CD=5,点E从点D出发,沿线段DA以每秒1个单位长的速度向点A方向移动,同时点F从点C出发,沿射线CD方向以每秒2个单位长的速度移动,当B、E、F三点共线时,两点同时停止运动,此时BF⊥CE.设点E移动的时间为t(秒).
如图,已知在矩形ABCD中,AD=10,CD=5,点E从点D出发,沿线段DA以每秒1个单位长的速度向点A方向移动,同时点F从点C出发,沿射线CD方向以每秒2个单位长的速度移动,当B、E、F三点共线时,两点同时停止运动,此时BF⊥CE.设点E移动的时间为t(秒).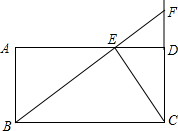 解:(1)当B,E,F三点共线时,两点同时停止运动,如图所示.
解:(1)当B,E,F三点共线时,两点同时停止运动,如图所示.| FD |
| FC |
| ED |
| BC |
| 2t-5 |
| 2t |
| t |
| 10 |
| BC |
| CD |
| CF |
| ED |
| 3 |
| 3 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
5
| ||
| 3 |
| 3 |
| 3 |
5
| ||
| 3 |
| 3 |


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
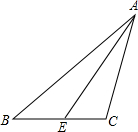 如图,△ABC中,∠B=36°,∠ACB=110°,AE是∠BAC的平分线.
如图,△ABC中,∠B=36°,∠ACB=110°,AE是∠BAC的平分线.查看答案和解析>>
科目:初中数学 来源: 题型:
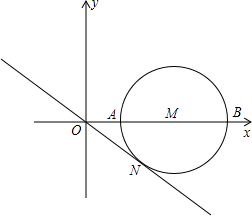 如图所示,在平面直角坐标中,M是x轴正半轴上一点,⊙M与x轴的正半轴交于A、B两点,A在B的左侧,且OA、OB的长是方程x2-4x+3=0的两根,ON是⊙M的切线,N为切点,N在第四象限.
如图所示,在平面直角坐标中,M是x轴正半轴上一点,⊙M与x轴的正半轴交于A、B两点,A在B的左侧,且OA、OB的长是方程x2-4x+3=0的两根,ON是⊙M的切线,N为切点,N在第四象限.查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
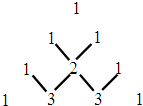 如图是我国古代数学家发现的,称为“杨辉三角形”,它的发现比西方要早五百年左右.“杨辉三角形”中有许多规律,如(a+b)2=a2+2ab+b2开式中的系数1、2、1恰好对应图中第三行的数字; (a+b)3=a3+3a2b+3ab2+b3展开式中的系数1、3、3、1恰好对应图中第四行的数字.请认真观察此图,写出(a+b)4的展开式.(a+b)4=
如图是我国古代数学家发现的,称为“杨辉三角形”,它的发现比西方要早五百年左右.“杨辉三角形”中有许多规律,如(a+b)2=a2+2ab+b2开式中的系数1、2、1恰好对应图中第三行的数字; (a+b)3=a3+3a2b+3ab2+b3展开式中的系数1、3、3、1恰好对应图中第四行的数字.请认真观察此图,写出(a+b)4的展开式.(a+b)4=查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com