
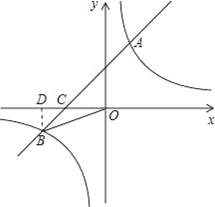
已知:如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数
 的图象交于一、三象限内的A、B两点,与x轴交于C点,点A的坐标为(2,m),点B的坐标为(n,﹣2),tan∠BOC=
的图象交于一、三象限内的A、B两点,与x轴交于C点,点A的坐标为(2,m),点B的坐标为(n,﹣2),tan∠BOC=
 .
.
(1)求该反比例函数和一次函数的解析式;
(2)在x轴上有一点E(O点除外),使得△BCE与△BCO的面积相等,求出点E的坐标.


【考点】反比例函数综合题.
【分析】(1)过B点作BD⊥x轴,垂足为D,由B(n,﹣2)得BD=2,由tan∠BOC=
 ,解直角三角形求OD,确定B点坐标,得出反比例函数关系式,再由A、B两点横坐标与纵坐标的积相等求n的值,由“两点法”求直线AB的解析式;
,解直角三角形求OD,确定B点坐标,得出反比例函数关系式,再由A、B两点横坐标与纵坐标的积相等求n的值,由“两点法”求直线AB的解析式;
(2)点E为x轴上的点,要使得△BCE与△BCO的面积相等,只需要CE=CO即可,根据直线AB解析式求CO,再确定E点坐标.
【解答】解:(1)过B点作BD⊥x轴,垂足为D,
∵B(n,﹣2),
∴BD=2,
在Rt△OBD中,tan∠BOC=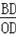
 ,即
,即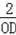
 =
=
 ,
,
解得OD=5,
又∵B点在第三象限,
∴B(﹣5,﹣2),
将B(﹣5,﹣2)代入y=
 中,得k=xy=10,
中,得k=xy=10,
∴反比例函数解析式为y=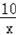
 ,
,
将A(2,m)代入y=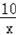
 中,得m=5,
中,得m=5,
∴A(2,5),
将A(2,5),B(﹣5,﹣2)代入y=ax+b中,
得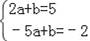
 ,
,
解得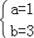
 .
.
则一次函数解析式为y=x+3;
(2)由y=x+3得C(﹣3,0),即OC=3,
∵S△BCE=S△BCO,
∴CE=OC=3,
∴OE=6,即E(﹣6,0).

【点评】本题考查了反比例函数的综合运用.关键是通过解直角三角形确定B点坐标,根据反比例函数图象上点的坐标特求A点坐标,求出反比例函数解析式,一次函数解析式.


科目:初中数学 来源: 题型:
某物质的密度ρ(kg/m3)关于其体积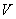 (m3)的函数图像如图所示,那么ρ与
(m3)的函数图像如图所示,那么ρ与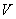 之间的函数表达式是 ( )
之间的函数表达式是 ( )
A. ρ=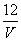 B. ρ=
B. ρ=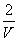 C. ρ=
C. ρ=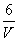 D.
D. 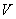 ρ=3
ρ=3
|
第2题 第4题 第5题 第7题 第8题
查看答案和解析>>
科目:初中数学 来源: 题型:
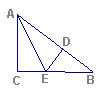
如右图,在△ABC中,∠ACB=90°,AE平分∠BAC,DE⊥AB于D,如果AC=3 cm, BC=4cm,AB=5,那么△EBD的周长等于为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com