
 如图,AD为⊙O的直径,CD为弦,$\widehat{AB}$=$\widehat{BC}$,连接OB.
如图,AD为⊙O的直径,CD为弦,$\widehat{AB}$=$\widehat{BC}$,连接OB.分析 (1)连接OC,根据$\widehat{AB}$=$\widehat{BC}$,得到∠BOA=$\frac{1}{2}∠$AOC,由圆周角定理得到$∠D=\frac{1}{2}∠$AOC,得到∠AOB=∠D,根据平行线的判定定理即可得到结论;
(2)连接AC交OB于M,由AD为⊙O的直径,得到∠ACD=90°,根据三角形的中位线的性质得到OM=$\frac{1}{2}$CD=$\frac{7}{2}$,然后根据勾股定理列方程即可得到结论.
解答 解:(1)连接OC,
∵$\widehat{AB}$=$\widehat{BC}$,
∴∠BOA=$\frac{1}{2}∠$AOC,
∵$∠D=\frac{1}{2}∠$AOC,
∴∠AOB=∠D,
∴OB∥CD;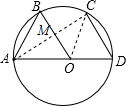
(2)连接AC交OB于M,
∵AD为⊙O的直径,
∴∠ACD=90°,
∵OB∥CD,∴∠AMO=90°,
∴AM=CM,
∵OA=OC,
∴OM=$\frac{1}{2}$CD=$\frac{7}{2}$,
∵AB=15,
设OA=OB=r,
∴AB2-BM2=AM2=OA2-OM2,
即152-(r-$\frac{7}{2}$)2=r2-($\frac{7}{2}$)2,
∴r=12.5,
∴⊙O的半径是12.5.
点评 本题考查了圆周角,弧,弦的关系,三角形的中位线的性质,勾股定理,正确的作出辅助线是解题的关键.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案科目:初中数学 来源: 题型:解答题
 如图,△ABC中,AC>AB,AE为外角∠FAC的角平分线,同时点E也在BC的垂直平分线上,若AB=AE,试判断∠ABC与∠ACB的数量关系,并加以证明.
如图,△ABC中,AC>AB,AE为外角∠FAC的角平分线,同时点E也在BC的垂直平分线上,若AB=AE,试判断∠ABC与∠ACB的数量关系,并加以证明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
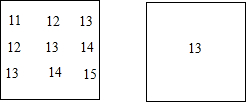 如图(1),方框内排列了一些数,若绕着它们的中心数13将这个数阵旋转180°.
如图(1),方框内排列了一些数,若绕着它们的中心数13将这个数阵旋转180°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com