
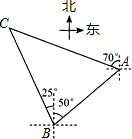
 如图,小岛A在港口B的北偏东50°方向,小岛C在港口B的北偏西25°方向,一艘轮船以每小时20海里的速度从港口B出发向小岛A航行,经过5小时到达小岛A,这时测得小岛C在小岛A的北偏西70°方向,求小岛A距离小岛C有多少海里?(最后结果精确到1海里,参考数据:$\sqrt{2}$≈1.1414,$\sqrt{3}$≈1.732)
如图,小岛A在港口B的北偏东50°方向,小岛C在港口B的北偏西25°方向,一艘轮船以每小时20海里的速度从港口B出发向小岛A航行,经过5小时到达小岛A,这时测得小岛C在小岛A的北偏西70°方向,求小岛A距离小岛C有多少海里?(最后结果精确到1海里,参考数据:$\sqrt{2}$≈1.1414,$\sqrt{3}$≈1.732) 分析 过点B作BD⊥AC,垂足为点D,根据题意求出∠ABC和∠BAC的度数以及AB的长,再求出AD和BD的长,结合CD=BD,即可求出AC的长.
解答 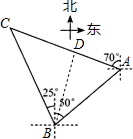 解:由题意得,∠ABC=25°+50°=75°,∠BAC=180°-70°-50°=60°,
解:由题意得,∠ABC=25°+50°=75°,∠BAC=180°-70°-50°=60°,
∴在△ABC中,∠C=45°,
过点B作BD⊥AC,垂足为点D,
∵AB=20×5=100,
在Rt△ABD中,∠BAD=60°,
∴BD=ABsin60°=100×$\frac{\sqrt{3}}{2}$=50$\sqrt{3}$,
∴AD=ABcos60°=100×$\frac{1}{2}$=50,
在Rt△BCD中,∠C=45°,
∴CD=BD=50$\sqrt{3}$,
∴AC=AD+CD=50+50$\sqrt{3}$≈137(海里),
答:小岛A距离小岛C约是137海里.
点评 此题考查了解直角三角形的应用-方向角问题的知识,解答此类题目的关键是构造出直角三角形,利用解直角三角形的相关知识解答,此题难度不大.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:解答题
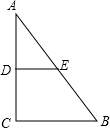 如图,在Rt△ABC中,∠C=90°,D是AC上一个动点,点E在AB上,DE∥BC,已知:AB=5,BC=3.设CD长为x,四边形CDEB面积为y,求y关于x的函数解析式,并写出定义域.
如图,在Rt△ABC中,∠C=90°,D是AC上一个动点,点E在AB上,DE∥BC,已知:AB=5,BC=3.设CD长为x,四边形CDEB面积为y,求y关于x的函数解析式,并写出定义域.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com