
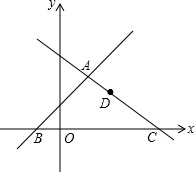
 如图,在平面直角坐标系xOy中,直线l1:y=x+1与直线l2:y=kx+3交于点A,分别交x轴于点B和点C(4,0),点D是直线l2上的一个动点,
如图,在平面直角坐标系xOy中,直线l1:y=x+1与直线l2:y=kx+3交于点A,分别交x轴于点B和点C(4,0),点D是直线l2上的一个动点,分析 (1)利用待定系数法求得函数解析式,把两条直线联立起来组成方程组,解方程组可得到A点坐标;再把y=0分别代入函数解析式可确定B点坐标;
(2)设出点D的坐标,根据${S_{△BCD}}=\frac{14}{15}{S_{△ABC}}$,列出方程解决问题;
(3)分类讨论:当DB=DC,则求得D点的横坐标,然后代入y=-$\frac{3}{4}$x+3可确定D点的纵坐标;当BC=BD=5,设D点坐标为(x、y),然后利用勾股定理建立等量关系求解.
解答 解:(1)将点C(4,0)代入y=kx+3,得4k+3=0,
$k=-\frac{3}{4}$,
直线l2的解析式为$y=-\frac{3}{4}x+3$,
解方程组$\left\{\begin{array}{l}y=x+1\\ y=-\frac{3}{4}x+3\end{array}\right.$,得$\left\{\begin{array}{l}x=\frac{8}{7}\\ y=\frac{15}{7}\end{array}\right.$,即$A(\frac{8}{7},\frac{15}{7})$,
由y=x+1,当y=0 时,x=-1,即B(-1,0);
(2)设点D的坐标为$(m,-\frac{3}{4}m+3)$,
${S_{△ABC}}=\frac{1}{2}BC•|{y_A}|=\frac{1}{2}×5×\frac{15}{7}=\frac{75}{14}$,
当${S_{△BCD}}=\frac{14}{15}{S_{△ABC}}=\frac{14}{15}×\frac{75}{14}=5$时,
即$\frac{1}{2}BC•|{-\frac{3}{4}m+3}|=5$
$|{-\frac{3}{4}m+3}|=2$,解得$m=\frac{4}{3}$或$m=\frac{20}{3}$,
当${S_{△BCD}}=\frac{14}{15}{S_{△ABC}}$时,点D的坐标为$(\frac{4}{3},2)$或$(\frac{20}{3},-2)$;
(3)①当BD=BC=5时,
即$\sqrt{{{(m+1)}^2}+{{(-\frac{3}{4}m+3)}^2}}=5$,
化简得5m2-8m-48=0,
即(m-4)(5m+12)=0,
解得:m1=4(此时点D与C重合,舍去),${m_2}=-\frac{12}{5}$;
②当CD=BC=5时,
即$\sqrt{{{(m-4)}^2}+{{(-\frac{3}{4}m+3)}^2}}=5$,
化简得m(m-8)=0,
m3=0,m4=8;
③当BD=CD时,${m_5}=\frac{4-1}{2}=\frac{3}{2}$,
综上所述,当△CBD为等腰三角形时,点D的坐标为$(-\frac{12}{5},\frac{24}{5})$,(0,3),$(\frac{3}{2},\frac{15}{8})$,(8,-3).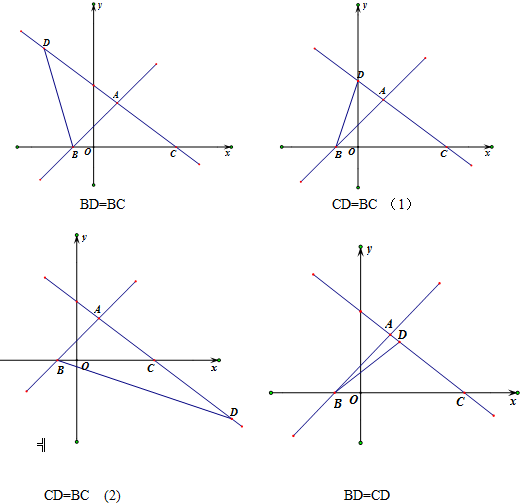
点评 此题考查了两直线平行或相交的问题:直线y=k1x+b1(k1≠0)和直线y=k2x+b2(k2≠0)平行,则k1=k2;若直线y=k1x+b1(k1≠0)和直线y=k2x+b2(k2≠0)相交,则交点坐标满足两函数的解析式.也考查了待定系数法求函数的解析式.


科目:初中数学 来源: 题型:选择题
| A. | 随机抽取一部分男生 | |
| B. | 随机抽取一个班级的学生 | |
| C. | 随机抽取一个年级的学生 | |
| D. | 在各个年级中,每班各随机抽取20名学生 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x>0 | B. | m>$\frac{1}{2}$ | C. | 0$<m<\frac{1}{2}$ | D. | -$\frac{1}{2}$<m<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com