
【题目】如图,在3×3的正方形网格中标出了∠1和∠2。则∠1+∠2=。 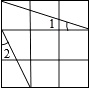
【答案】45°
【解析】解 :连接AC,BC .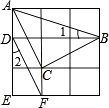
根据勾股定理,AC=BC=![]() ;AB=
;AB=![]()
∵(![]() )2+(
)2+(![]() )2=(
)2=(![]() )2 ,
)2 ,
∴△ABC是等腰直角三角形,
∴∠ACB=90,∠CAB=45.
∵AD∥CF,AD=CF,
∴四边形ADFC是平行四边形,
∴AC∥DF,
∴∠2=∠DAC;
在Rt△ABD中,
∠1+∠DAB=90;
又∵∠DAB=∠DAC+∠CAB,
∴∠1+∠CAB+∠DAC=90 ,
∴∠1+∠DAC=45 ,
∴∠1+∠2=∠1+∠DAC=45.
故答案为:45.
连接AC,BC ;利用方格纸的特点,根据勾股定理得出AC,BC,AB的长, 然后根据勾股定理的逆定理判断出 △ABC是等腰直角三角形,从而得出 ∠ACB=90,∠CAB=45.根据一组对边平行且相等的四边形是平行四边形得出 四边形ADFC是平行四边形,根据平行四边形的对边平行得出AC∥DF,根据二直线平行同位角相等得出∠2=∠DAC;根据直角三角形两锐角互余得出∠1+∠DAB=90;,根据角的和差及等量代换得出∠1+∠2=∠1+∠DAC=45.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,按以下步骤作图:①分别以A、B为圆心,大于![]() AB的长为半径画弧,两弧相交于点M、N;②作直线MN交AC于点D,连接BD.若CD=CB,∠A=35°,则∠C等于( )
AB的长为半径画弧,两弧相交于点M、N;②作直线MN交AC于点D,连接BD.若CD=CB,∠A=35°,则∠C等于( )

A. 40° B. 50° C. 60° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设x1 , x2 , x3 , x4 , x5 , x6 , x7是自然数,且x1<x2<x3<x4<x5<x6<x7 , x1+x2=x3 , x2+x3=x4 , x3+x4=x5 , x4+x5=x6 , x5+x6=x7 , 又x1+x2+x3+x4+x5+x6+x7=2010,那么x1+x2+x3的值最大是。
查看答案和解析>>
科目:初中数学 来源: 题型:
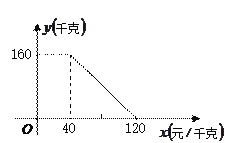
【题目】某商店以40元/千克的进价购进一批茶叶,经调查发现,在一段时间内,销售量![]() (千克)与销售价
(千克)与销售价![]() (元/千克)成一次函数关系,其图象如图所示.
(元/千克)成一次函数关系,其图象如图所示.
(1)求![]() 与
与![]() 之间的函数关系式(不必写出自变量
之间的函数关系式(不必写出自变量![]() 的取值范围);
的取值范围);
(2)若该商店销售这批茶叶的成本不超过2800元,则它的最低销售价应定为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com